题目内容
如图,在直角坐标系xOy中,已知椭圆![]() 的离心率e=
的离心率e=![]() ,左右两个焦分别为F1、F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=1.
,左右两个焦分别为F1、F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=1.

(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左顶点为A,下顶点为B,动点P满足![]() ,(
,(![]() )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
答案:
解析:
解析:
解:(Ⅰ)∵![]() 轴,∴
轴,∴![]() ,由椭圆的定义得:
,由椭圆的定义得:![]() , 2分
, 2分
∵![]() ,∴
,∴![]() , 4分
, 4分
又![]() 得
得![]() ∴
∴![]()
![]()
![]()
∴![]() , 6分
, 6分
∴所求椭圆C的方程为![]() . 7分;
. 7分;
(Ⅱ)由(Ⅰ)知点A(-2,0),点B为(0,-1),设点P的坐标为![]() 则
则![]() ,
,![]() ,由
,由![]() -4得-
-4得-![]() ,
,
∴点P的轨迹方程为![]() 9分
9分
设点B关于P的轨迹的对称点为![]() ,则由轴对称的性质可得:
,则由轴对称的性质可得:![]() ,
,
解得:![]() , 11分
, 11分
∵点![]() 在椭圆上,∴
在椭圆上,∴![]() ,整理得
,整理得![]() 解得
解得![]() 或
或![]()
∴点P的轨迹方程为![]() 或
或![]() , 13分
, 13分
经检验![]() 和
和![]() 都符合题设,
都符合题设,
∴满足条件的点P的轨迹方程为![]() 或
或![]() . 14分
. 14分

练习册系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.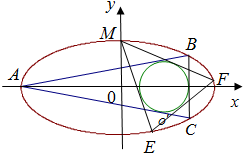 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且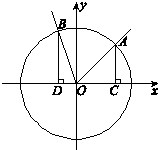 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: