题目内容
给出下列五个命题:①函数
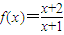 的图象的对称中心是点(1,1);②函数y=sinx在第一象限内是增函数;③已知a,b,m均是负数,且
的图象的对称中心是点(1,1);②函数y=sinx在第一象限内是增函数;③已知a,b,m均是负数,且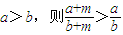 ;④若直线l∥平面α,直线l⊥直线m,直线m?平面β,则β⊥α;⑤当椭圆的离心率e越接近于0时,这个椭圆的形状就越接近于圆.其中正确命题的序号为 .
;④若直线l∥平面α,直线l⊥直线m,直线m?平面β,则β⊥α;⑤当椭圆的离心率e越接近于0时,这个椭圆的形状就越接近于圆.其中正确命题的序号为 .
【答案】分析:①将函数分离常数,利用图象变换可得其对称中心;②举反例即可否定此选项,例如举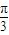 ,
,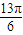 都是第一象限角;③利用作差比较法证明其正确;④在正方体中寻找反例即可否定此结论;⑤由椭圆离心率的定义e=
都是第一象限角;③利用作差比较法证明其正确;④在正方体中寻找反例即可否定此结论;⑤由椭圆离心率的定义e=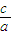 ,推导出当椭圆的离心率e越接近于0时,椭圆长轴2a就越接近于短轴2b,椭圆的形状就越接近于圆
,推导出当椭圆的离心率e越接近于0时,椭圆长轴2a就越接近于短轴2b,椭圆的形状就越接近于圆
解答:解:∵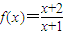 =
=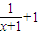 ,∴图象为y=
,∴图象为y=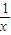 图象向左平移1个单位,再向上平移1个单位,∴对称中心是(-1,1)
图象向左平移1个单位,再向上平移1个单位,∴对称中心是(-1,1)
∴①错误
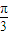 ,
,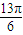 都是第一象限角,且
都是第一象限角,且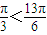 ,但sin
,但sin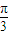 >sin
>sin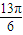 ,∴不能说函数y=sinx在第一象限内是增函数.
,∴不能说函数y=sinx在第一象限内是增函数.
∴②错误
∵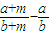 =
=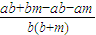 =
=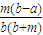 ,∵,b,m均是负数,且a>b,∴
,∵,b,m均是负数,且a>b,∴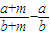 >0∴
>0∴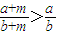
∴③正确
例如在正方体ABCD-A1B1C1D1中,AC∥平面A1C1,AC⊥BD,BD⊆平面BDC1,但平面A1C1与平面BDC1并不垂直
∴④错误
e2=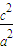 =
=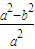 =1-
=1-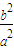 ,当e越接近于0时,
,当e越接近于0时,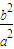 就越接近1,a就越接近b,椭圆的形状就越接近于圆,
就越接近1,a就越接近b,椭圆的形状就越接近于圆,
∴⑤正确
故答案为③⑤
点评:本题通过多选的形式,考查了三角函数,图象变换,不等式证明,空间线面关系,椭圆等基础知识,属于基础题
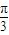 ,
,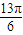 都是第一象限角;③利用作差比较法证明其正确;④在正方体中寻找反例即可否定此结论;⑤由椭圆离心率的定义e=
都是第一象限角;③利用作差比较法证明其正确;④在正方体中寻找反例即可否定此结论;⑤由椭圆离心率的定义e=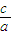 ,推导出当椭圆的离心率e越接近于0时,椭圆长轴2a就越接近于短轴2b,椭圆的形状就越接近于圆
,推导出当椭圆的离心率e越接近于0时,椭圆长轴2a就越接近于短轴2b,椭圆的形状就越接近于圆解答:解:∵
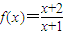 =
=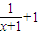 ,∴图象为y=
,∴图象为y=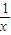 图象向左平移1个单位,再向上平移1个单位,∴对称中心是(-1,1)
图象向左平移1个单位,再向上平移1个单位,∴对称中心是(-1,1)∴①错误
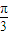 ,
,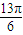 都是第一象限角,且
都是第一象限角,且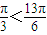 ,但sin
,但sin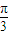 >sin
>sin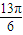 ,∴不能说函数y=sinx在第一象限内是增函数.
,∴不能说函数y=sinx在第一象限内是增函数.∴②错误
∵
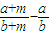 =
=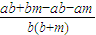 =
=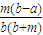 ,∵,b,m均是负数,且a>b,∴
,∵,b,m均是负数,且a>b,∴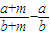 >0∴
>0∴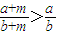
∴③正确
例如在正方体ABCD-A1B1C1D1中,AC∥平面A1C1,AC⊥BD,BD⊆平面BDC1,但平面A1C1与平面BDC1并不垂直
∴④错误
e2=
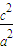 =
=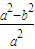 =1-
=1-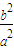 ,当e越接近于0时,
,当e越接近于0时,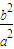 就越接近1,a就越接近b,椭圆的形状就越接近于圆,
就越接近1,a就越接近b,椭圆的形状就越接近于圆,∴⑤正确
故答案为③⑤
点评:本题通过多选的形式,考查了三角函数,图象变换,不等式证明,空间线面关系,椭圆等基础知识,属于基础题

练习册系列答案
相关题目