题目内容
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则△ABC是( )
| A.等腰三角形 | B.直角三角形 |
| C.等边三角形 | D.等腰直角三角形 |
A
解析试题分析:因为lg sin A-lg cos B-lg sin C=lg 2,所以lg sin A=lg 2 cos B sin C,即sin A=2 cos B sin C,又由于sin A=sin ( B + C)=sinBcosC+cosBsinC,故sinBcosC+cosBsinC ="2" cos B sin C,所以sinBcosC-cos B sin C=0,所以sin(B-C)=0,由于B、C为三角形的内角,所以B=C,即三角形ABC为等腰三角形.
考点:1.正弦定理;2.两角和差公式.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
设△ABC的内角A, B, C所对的边分别为a, b, c, 若 , 则△ABC的形状是 ( )
, 则△ABC的形状是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不确定 |
在 中,边
中,边 所对角分别为
所对角分别为 ,若
,若 ,则
,则
A. | B. | C. | D. |
符合下列条件的三角形有且只有一个的是( )
| A.a=1, b="2" , c=3 | B.a=1, b=2,∠A=100° |
C.a=1, b= , ∠A=30° , ∠A=30° | D.b="c=1," ∠B=45° |
△ABC中,a=18,c=25,B=30°,则△ABC的面积为( )
| A.450 | B.900 | C.450 | D.900 |
在△ABC中,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
 ABC中,若cos2A=cos2B,则
ABC中,若cos2A=cos2B,则 ,若
,若 ,则
,则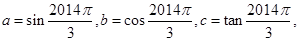 则
则
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 =2cos(3x+
=2cos(3x+
 m
m m
m m
m a+c,sinB-sinA),若m∥n,则角B的大小为( )
a+c,sinB-sinA),若m∥n,则角B的大小为( )