题目内容
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是( )
| A.10m |
B.10 m m |
C.10 m m |
D.10 m m |
D
解析

练习册系列答案
相关题目
设 的内角
的内角 所对边的长分别为
所对边的长分别为 ,若
,若 ,则角
,则角 =( )
=( )
A. | B. | C. | D. |
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则△ABC是( )
| A.等腰三角形 | B.直角三角形 |
| C.等边三角形 | D.等腰直角三角形 |
在△ABC中,A=45°,B=30o,b=2,则a的值为( )
| A.4 | B.2 | C. | D.3 |
在△ABC中,内角A、B、C的对边分别是a、b、c,若 ,
, ,则A=( )
,则A=( )
| A.30° | B.60° |
| C.120° | D.150° |
(2014·宜昌模拟)在△ABC中,若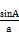 =
=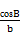 ,则B的值为( )
,则B的值为( )
| A.30° | B.45° | C.60° | D.90° |
在△ABC中,角A,B,C所对的边长分别为a,b,c.若C=120°,c= a,则( )
a,则( )
| A.a>b |
| B.a<b |
| C.a=b |
| D.a与b的大小关系不能确定 |
 B.
B.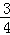 C.
C.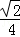 D.
D.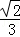
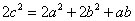 ,则△ABC是( )
,则△ABC是( )