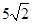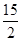题目内容
对于函数f (x)和g(x),其定义域为[a, b],若对任意的x∈[a, b]总有|1- |≤
|≤ ,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)=
,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)= x∈[4,16]的是 ( )
x∈[4,16]的是 ( )
| A.g(x)=2x+6 x∈[4,16] | B.g(x)=x2+9 x∈[4,16] |
C.g(x)=  (x+8) x∈[4,16] (x+8) x∈[4,16] | D.g(x)= (x+6) x∈[4,16] (x+6) x∈[4,16] |
D
解析试题分析:由题意可知:当g(x)=2x+6,x∈[4,16]时,令x=4,可得|1- |=6>
|=6> ,不符合要求;当g(x)=x2+9,x∈[4,16], 令x=4,可得|1-
,不符合要求;当g(x)=x2+9,x∈[4,16], 令x=4,可得|1- |=
|=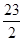 >
> ,不符合要求;
,不符合要求;
当g(x)= (x+8),x∈[4,16]时,令x=4,可得|1-
(x+8),x∈[4,16]时,令x=4,可得|1- |=1>
|=1> ,不符合要求;当g(x)=
,不符合要求;当g(x)= (x+6) x∈[4,16]时满足要求.
(x+6) x∈[4,16]时满足要求.
考点:本小题主要考查函数的值域问题,考查对新定义的理解和应用问题.
点评:新定义问题一般是新而不难,仔细读题,合理转化即可.

练习册系列答案
相关题目
已知函数 是奇函数,当
是奇函数,当 时,
时, ,则
,则 的值为
的值为
A. | B. | C. | D. |
函数 的零点个数
的零点个数
| A.0 | B.1 |
| C.2 | D.1或2 |
已知函数
 ,则函数( )
,则函数( )
A.是奇函数,在 上是减函数 上是减函数 |
B.是偶函数,在 上是减函数 上是减函数 |
C.是奇函数,在 上是增函数 上是增函数 |
D.是偶函数,在 上是增函数 上是增函数 |
下列函数是偶函数的是( )
A.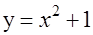 , ,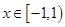 | B.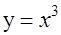 |
C. | D. |
下列函数中,在区间 上是增函数的是 ( )
上是增函数的是 ( )
A. | B. | C. | D. |
设函数 为偶函数,则
为偶函数,则 ( )
( )
| A.1 | B. | C.0 | D.2 |
已知函数 的定义域为M,
的定义域为M, 的定义域为N,则M
的定义域为N,则M
 =
=
A.{ } } | B.{ } } |
C. | D.( }) }) |
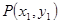 、
、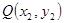 之间的“理想距离”为:
之间的“理想距离”为: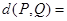
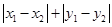 ;若
;若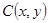 到点
到点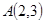 、
、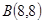 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数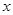 、
、 满足
满足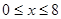 、
、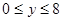 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长度之和是
的轨迹的长度之和是