题目内容
已知向量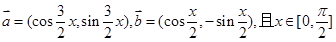 ,
,
(1)求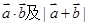 ;
;
(2)若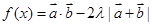 的最小值是
的最小值是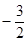 ,求实数
,求实数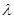 的值.
的值.
(1)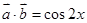 ,
,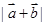 =2cosx(2)
=2cosx(2)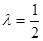
解析试题分析:(1)由向量的坐标运算,利用公式化简即可;(2)原函数由向量坐标运算可化为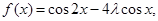 即
即 又最小值
又最小值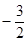 ,则结合二次函数最值可求得
,则结合二次函数最值可求得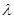 .
.
试题解析:解:(1) =
=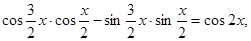
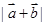 =
=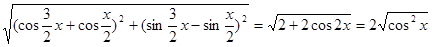 ,
,
∵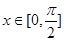 ,∴
,∴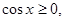
∴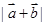 =2cosx. 6分
=2cosx. 6分
(2)由(1)得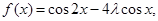
即
∵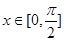 ,∴
,∴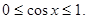
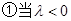 时,当且仅当
时,当且仅当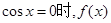 取得最小值-1,这与已知矛盾.
取得最小值-1,这与已知矛盾.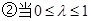 时,当且仅当
时,当且仅当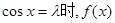 取最小值
取最小值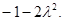
由已知得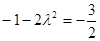 ,解得
,解得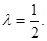
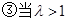 时,当且仅当
时,当且仅当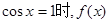 取得最小值
取得最小值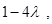
由已知得 ,解得
,解得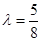 ,这与
,这与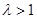 相矛盾.
相矛盾.
综上所述,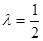 为所求. 12分
为所求. 12分
考点:向量的坐标运算,二次函数求最值,函数与方程的数学思想,分类讨论的数学思想.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
[2013·江西抚州月考]数列{an}的前n项积为n2,那么当n≥2时,{an}的通项公式为( )
| A.an=2n-1 | B.an=n2 |
C.an= | D.an= |
 中,
中,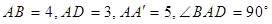 ,
, ,则
,则 的长是
的长是 
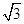 ,-1).
,-1).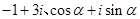 (
(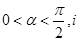 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为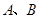 ,点
,点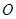 是坐标原点.
是坐标原点. ,求
,求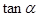 的值;
的值; 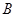 点的横坐标为
点的横坐标为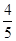 ,求
,求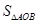 .
. ,
, ,
, ,其中
,其中
 ,试求
,试求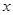 与
与 之间的表达式;
之间的表达式; ,试求
,试求 的面积。
的面积。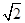 ,求证:a⊥b;
,求证:a⊥b;