题目内容
下列函数中,对于任意的x(x∈R),都有f(-x)=f(x),且在区间(0,1)上单调递增的是( )A.f(x)=-x2+2
B.f(x)=

C.f(x)=x2-1
D.f(x)=x3
【答案】分析:由已知可得满足条件的函数是偶函数,且在区间(0,1)上单调递增,根据二次函数,指数函数和幂函数的图象和性质,分别分析四个答案中的函数是否满足上述两个条件,可得答案.
解答:解:∵对于任意的x(x∈R),都有f(-x)=f(x),故函数f(x)为偶函数
A中,f(x)=-x2+2为偶函数,但在区间(0,1)上单调递减;
B中,f(x)=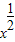 在区间(0,1)上单调递增,但是非奇非偶函数;
在区间(0,1)上单调递增,但是非奇非偶函数;
C中,f(x)=x2-1为偶函数,且在区间(0,1)上单调递增;
D中,f(x)=x3在区间(0,1)上单调递增,但是奇函数;
故选C
点评:本题考查的知识点是函数的单调性及单调区间,熟练掌握各种基本初等函数的图象和性质是解答的关键.
解答:解:∵对于任意的x(x∈R),都有f(-x)=f(x),故函数f(x)为偶函数
A中,f(x)=-x2+2为偶函数,但在区间(0,1)上单调递减;
B中,f(x)=
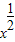 在区间(0,1)上单调递增,但是非奇非偶函数;
在区间(0,1)上单调递增,但是非奇非偶函数;C中,f(x)=x2-1为偶函数,且在区间(0,1)上单调递增;
D中,f(x)=x3在区间(0,1)上单调递增,但是奇函数;
故选C
点评:本题考查的知识点是函数的单调性及单调区间,熟练掌握各种基本初等函数的图象和性质是解答的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列函数中,对于任意x∈R,同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )
| A、f(x)=sinx | B、f(x)=sin2x | C、f(x)=cosx | D、f(x)=cos2x |
