题目内容
【题目】商品的销售价格与销售量密切相关，为更精准地为商品确定最终售价，商家对商品A按以下单价进行试售，得到部分的数据如下：
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
（1）求销量
关于
的线性回归方程；
（2）预计今后的销售中，销量与单价服从（1）中的线性回归方程，已知每件商品
的成本是
元，为了获得最大利润，商品的单价应定为多少元？（结果保留整数）
参考数据：
，
，
）（参考公式：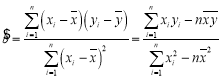
，
）
【答案】（1）
；（2）
元.
【解析】
（1）求出
和
的值，将表格中的数据代入最小二乘法公式求出
和
的值，即可求出回归直线方程；
（2）设商品
的单价应定为
元，可得出利润
关于的函数解析式为
，再由二次函数的基本性质求最值．
（1）
，
，
，
.
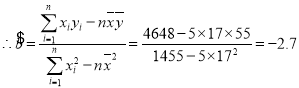销量
关于的线性回归方程为；
（2）设商品的单价应定为元，则利润
，
当
时，获得的利润最大．
练习册系列答案
阅读快车系列答案
相关题目
【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到频数分布表和频率分布直方图如下．
组号 | 分组 | 频数 |
1 | [0，2） | 6 |
2 | [2，4） | 8 |
3 | [4，6） | 17 |
4 | [6，8） | 22 |
5 | [8，10） | 25 |
6 | [10，12） | 12 |
7 | [12，14） | 6 |
8 | [14，16） | 2 |
9 | [16，18） | 2 |
合计 | 100 |
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的频率；
（2）求频率分布直方图中的a，b的值．