题目内容
14.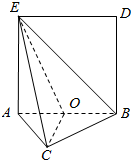 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.(1)在线段BD上是否存在点F,使得AF⊥平面EOC,证明你的结论;
(2)求二面角B-EC-O的余弦值.
分析 (1)以O为原点,OC为x轴,OB为y轴,建立如图所示的空间直角坐标系,利用向量法能求出在线段BD上存在点F,使得AF⊥平面EOC.
(2)分别求出平面BEC的法向量和平面ECO的法向量,利用向量法能求出二面角B-EC-O的余弦值.
解答 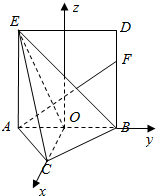 解:(1)在线段BD上不存在点F,使得AF⊥平面EOC.
解:(1)在线段BD上不存在点F,使得AF⊥平面EOC.
证明如下:
以O为原点,OC为x轴,OB为y轴,建立如图所示的空间直角坐标系,
由已知得A(0,-$\sqrt{3}$,0),O(0,0,0),C(3,0,0),
E(0,-$\sqrt{3}$,3),设F(0,$\sqrt{3}$,t),0≤t≤3,
$\overrightarrow{OE}$=(0,-$\sqrt{3}$,3),$\overrightarrow{OC}$=(3,0,0),$\overrightarrow{AF}$=(0,2$\sqrt{3}$,t),
设平面ECO的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OE}=-\sqrt{3}y+3z=0}\\{\overrightarrow{n}•\overrightarrow{OC}=3x=0}\end{array}\right.$,取y=$\sqrt{3}$,得$\overline{n}$=(0,$\sqrt{3}$,1),
当AF⊥平面EOC时,$\overrightarrow{n}∥\overrightarrow{AF}$,∴t=2,不满足0≤t≤3,
∴在线段BD上存在点F,使得AF⊥平面EOC.
(2)B(0,$\sqrt{3}$,0),$\overrightarrow{BE}=(0,-2\sqrt{3},3)$,$\overrightarrow{BC}$=(3,-$\sqrt{3}$,0),
设平面BEC的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BE}=-2\sqrt{3}b+3c=0}\\{\overrightarrow{m}•\overrightarrow{BC}=3a-\sqrt{3}b=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,$\sqrt{3}$,2),
由(1)得平面ECO的法向量$\overrightarrow{n}$=(0,$\sqrt{3}$,1),
设二面角B-EC-O的平面角为θ,
则cosθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{0+3+2}{\sqrt{8}•\sqrt{4}}$|=$\frac{5\sqrt{2}}{8}$.
∴二面角B-EC-O的余弦值为$\frac{5\sqrt{2}}{8}$.
点评 本题考查直线与平面垂直的判断与证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 阅读快车系列答案
阅读快车系列答案 如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.
如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.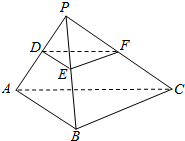 已知D,E,F分别是三棱锥P-ABC的棱PA,PB,PC的中点,求证:平面DEF∥平面ABC.
已知D,E,F分别是三棱锥P-ABC的棱PA,PB,PC的中点,求证:平面DEF∥平面ABC.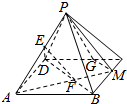 如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM.
如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM. 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.