题目内容
【题目】某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”.
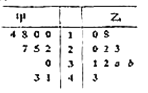
(Ⅰ)求在这10个卖场中,甲型号汽车的“星级卖场”的个数;
(Ⅱ)若在这10个卖场中,乙型号汽车销售量的平均数为26.7,求![]() 的概率;
的概率;
(Ⅲ)若![]() ,记乙型号汽车销售量的方差为
,记乙型号汽车销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值(只写出结论).
达到最小值(只写出结论).
注:方差![]() ,其中
,其中![]() 是
是![]() ,
,![]() ,…,
,…,![]() 的平均数.
的平均数.
【答案】(1)5
(2)![]()
(3)![]()
【解析】
(Ⅰ)根据茎叶图,代入即可求得甲型号汽车的平均值,即可求得“星级卖场”的个数;
(Ⅱ)根据乙组数据的平均值,可代入求得![]() .由古典概型概率,列举出所有可能,即可求得符合
.由古典概型概率,列举出所有可能,即可求得符合![]() 的概率.
的概率.
(Ⅲ)当![]() 时,由方差公式可知,当
时,由方差公式可知,当![]() 的值越小,其方差值越小,即
的值越小,其方差值越小,即![]() 时方差
时方差![]() 取得最小值.
取得最小值.
(1)根据茎叶图得到甲组数据的平均值:
![]() .
.
该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”,
在这10个卖场中,甲型号汽车的“星级卖场”的个数为5个.
(2)记事件![]() 为“
为“![]() ”,乙组数据的平均值:
”,乙组数据的平均值:
![]()
![]() ,
,
∴![]() ,
,
和取值共9种,分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其
,其![]() 的有4种,
的有4种,
∴![]() 的概率
的概率![]() .
.
(3)由题意可知当![]() 的值越小,其方差值越小
的值越小,其方差值越小
所以![]() 时,
时,![]() 达到最小值.
达到最小值.

【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区 | 愿意参加 | 不愿意参加 |
重庆一中本部校区 | 220 | 980 |
重庆一中大学城校区 | 80 | 720 |
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分![]() 的概率满足:
的概率满足:![]() ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,
①对于一道不完全会的题,求“如花姐”得分的均值![]() ;
;
②试求“如花姐”在本次摸底考试中总得分的数学期望.