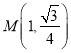题目内容
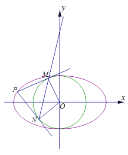
【题目】如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且![]() ,
,![]() .
.
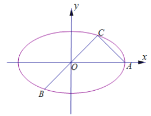
(Ⅰ)求椭圆E的方程;
(Ⅱ)设![]() 是以原点为圆心,短轴长为半径的圆,过椭圆E上异于其顶点的任一点P,作
是以原点为圆心,短轴长为半径的圆,过椭圆E上异于其顶点的任一点P,作![]() 的两条切线,切点分别为M,N,若直线MN在x轴、y轴上的截距分别为m,n,试计算
的两条切线,切点分别为M,N,若直线MN在x轴、y轴上的截距分别为m,n,试计算![]() 的值是否为定值?如果是,请给予证明;如果不是,请说明理由.
的值是否为定值?如果是,请给予证明;如果不是,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)是定值,证明见解析.
;(Ⅱ)是定值,证明见解析.
【解析】
(Ⅰ)由已知得![]() ,数形结合求得
,数形结合求得![]() 的坐标,代入椭圆方程求得
的坐标,代入椭圆方程求得![]() ,则椭圆方程可求;
,则椭圆方程可求;
(Ⅱ)设![]() ,
,![]() ,由
,由![]() ,
,![]() 是切点,可知
是切点,可知![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.分别写出以
四点共圆.分别写出以![]() 为直径的圆的方程与圆
为直径的圆的方程与圆![]() 的方程,联立可得
的方程,联立可得![]() 所在直线方程求出直线
所在直线方程求出直线![]() 在
在![]() ,
,![]() 轴上的截距,结合
轴上的截距,结合![]() 在椭圆上可得
在椭圆上可得![]() 的值是定值.
的值是定值.
解:(Ⅰ)依题意知:椭圆的长半轴长![]() ,则
,则![]() ,
,
设椭圆![]() 的方程为
的方程为![]()
由椭圆的对称性知![]() ,又
,又![]()
![]()
![]() ,
,![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 点C的坐标为
点C的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,
将C的坐标![]() 代入椭圆方程得
代入椭圆方程得![]()
![]() 所求的椭圆
所求的椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设点![]() ,由
,由![]() ,
,![]() 是
是![]() 的切点知,
的切点知,![]() ,
,![]() ,
,
![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一圆上,
四点在同一圆上,
且圆的直径为OP则圆心为![]() ,
,
其方程为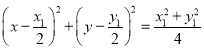 ,
,
即![]() ①
①
即点![]() ,
,![]() 满足方程①,又点
满足方程①,又点![]() ,
,![]() 都在
都在![]() 上,
上,
![]() ,
, ![]() 坐标也满足方程
坐标也满足方程![]() ②
②
②![]() ①得直线
①得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() 得
得![]() ,
,
![]() ,
,![]() ,又点Р在椭圆E上,
,又点Р在椭圆E上,
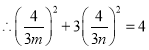 ,即
,即![]() 为定值.
为定值.

练习册系列答案
相关题目