Question

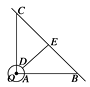
【题目】为了适应市场需要，某地准备建一个圆形生猪储备基地(如右图)，它的附近有一条公路，从基地中心O处向东走1 km是储备基地的边界上的点A ， 接着向东再走7 km到达公路上的点B；从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D ， 修建一条由D通往公路BC的专用线DE ， 求DE的最短距离.

Answer 1

【答案】解:以O为坐标原点，过OB、OC的直线分别为x轴和y轴，建立平面直角坐标系，

则圆O的方程为x2＋y2＝1，因为点B(8,0)、C(0,8)，所以直线BC的方程为 ＝1，即x＋y＝8.

当点D选在与直线BC平行的直线(距BC较近的一条)与圆相切所成切点处时，DE为最短距离，此时DE的最小值为 －1＝(4 －1)km.

【解析】先根据题意建立适当的直角坐标系，在这个坐标系中表示出圆O与点B，C的坐标，从而表示出直线BC的方程；求线段DE的方法为：过O作OE垂直于直线BC，垂足为E，交圆O与点D则DE即为所求，从而DE的长度为线段OE与圆O半径的差.