题目内容
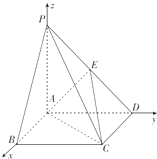
【题目】在如图所示的四棱锥P﹣ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E,M,N分别为PD,CD,AD的中点, ![]() =3
=3 ![]() .
. 
(1)证明:PB∥平面FMN;
(2)若PA=AB,求二面角E﹣AC﹣B的余弦值. 
【答案】
(1)证明:连结BD,分别交AC、MN于点O,G,连结EO、FG,
∵O为BD中点,E为PD中点,∴EO∥PB,
又 ![]() =3
=3 ![]() ,∴F为ED中点,又CM=MD,AN=DN,∴G为OD的中点,
,∴F为ED中点,又CM=MD,AN=DN,∴G为OD的中点,
∴FG∥EO,∴PB∥FG,
∵FG平面FMN,PB平面FMN,
∴PB∥平面FMN.
(2)解:∵BC⊥平面PAB,∴BC⊥PA,又PA⊥CD,BC∩CD=C,
∴PA⊥平面ABCD,
如图,以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
设PA=AB=2,则A(0,0,0),B(2,0,0),C(2,2,0),E(0,1,1),
则 ![]() =(2,2,0),
=(2,2,0), ![]() =(0,1,1),
=(0,1,1),
平面ABCD的一个向向量 ![]() =(0,0,1),
=(0,0,1),
设平面AEC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 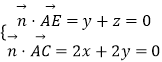 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,1),
=(1,﹣1,1),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
由图知二面角E﹣AC﹣B为钝角,
∴二面角E﹣AC﹣B的余弦值为﹣ ![]() .
.
【解析】(1)连结BD,分别交AC、MN于点O,G,连结EO、FG,推导出EO∥PB,FG∥EO,PB∥FG,由此能证明PB∥平面FMN.(2)以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,由此能求出二面角E﹣AC﹣B的余弦值.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?