题目内容
设函数 。
。
(1)如果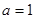 ,求函数
,求函数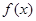 的单调递减区间;
的单调递减区间;
(2)若函数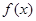 在区间
在区间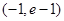 上单调递增,求实数
上单调递增,求实数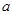 的取值范围;
的取值范围;
(3)证明:当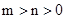 时,
时,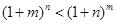
 。
。(1)如果
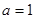 ,求函数
,求函数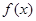 的单调递减区间;
的单调递减区间;(2)若函数
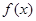 在区间
在区间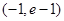 上单调递增,求实数
上单调递增,求实数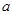 的取值范围;
的取值范围;(3)证明:当
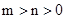 时,
时,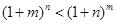
(1)函数的单调减区间为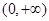 .(2)
.(2)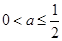 .(3)分析法
.(3)分析法
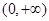 .(2)
.(2)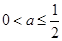 .(3)分析法
.(3)分析法试题分析:首先求导数,
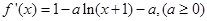
讨论得到当
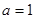 时,
时, ,确定函数的单调减区间为
,确定函数的单调减区间为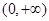 .
.(2)注意讨论①当
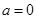 时,情况特殊;②当
时,情况特殊;②当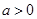 时,令
时,令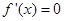 ,求驻点,讨论
,求驻点,讨论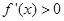 时,得函数的增区间为
时,得函数的增区间为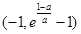 ;
;根据函数
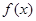 在区间
在区间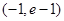 上单调递增,得到
上单调递增,得到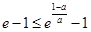 ,得出所求范围..
,得出所求范围..(3)利用分析法,转化成证明
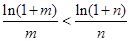 ;
;构造函数
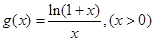 ,
,应用导数知识求解
试题解析:(1)函数的定义域为
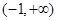 ,
,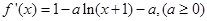
当
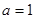 时,
时,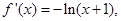
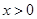 时,
时, ,所以,函数的单调减区间为
,所以,函数的单调减区间为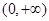 .
.(2)①当
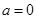 时,
时,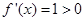 ,所以,函数的单调增区间为
,所以,函数的单调增区间为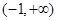 ;
;②当
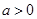 时,令
时,令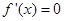 ,得
,得 ,
,当
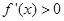 时,得
时,得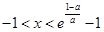 ,函数的增区间为
,函数的增区间为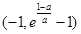 ;
;又因为,函数
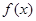 在区间
在区间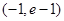 上单调递增,
上单调递增,所以,
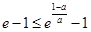 ,得
,得 ,综上知,
,综上知,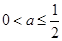 .
.(3)要证:
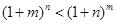 只需证
只需证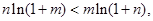
只需证
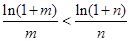
设
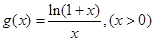 ,
, 则
 11分
11分由(1)知:即当
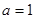 时,
时,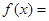
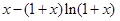 在
在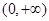 单调递减,
单调递减,即
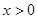 时,有
时,有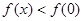 , 12分
, 12分∴
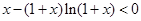 ,所以
,所以
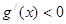 ,即
,即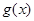 是
是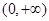 上的减函数, 13分
上的减函数, 13分即当
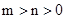 ,∴
,∴ ,故原不等式成立。 14分
,故原不等式成立。 14分
练习册系列答案
相关题目
 。
。 的单调区间;
的单调区间; ,证明当
,证明当 时,函数
时,函数 图象的上方.
图象的上方.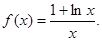
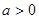 且函数
且函数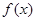 在区间
在区间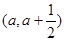 上存在极值,求实数
上存在极值,求实数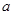 的取值范围;
的取值范围;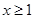 时,不等式
时,不等式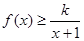 恒成立,求实数
恒成立,求实数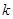 的取值范围.
的取值范围.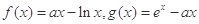 ,其中a为正实数.
,其中a为正实数. 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性; 上无最小值,且
上无最小值,且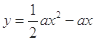 在
在 +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1, )(n≥2),求证:
)(n≥2),求证: <
< <
< .
. .
. ,求
,求 的极值;
的极值; 的取值范围.
的取值范围.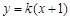 与曲线
与曲线 相切于点
相切于点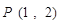 ,则
,则 ________.
________.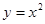 在
在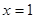 处的切线与两坐标轴围成三角形区域为
处的切线与两坐标轴围成三角形区域为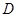 (包含三角形内部与边界).若点
(包含三角形内部与边界).若点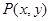 是区域
是区域 的取值范围是__________.
的取值范围是__________.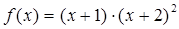 的导函数为
的导函数为