已知函数$f(x)=\left\{\begin{array}{l}{x^2}+4x.x≥0\\ 4x-{x^2}.x＜0\end{array}\right.$.若f(2-a2)＞f(a).则实数a的取值范围是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

4．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+4x，x≥0\\ 4x-{x^2}，x＜0\end{array}\right.$，若f（2-a²）＞f（a），则实数a的取值范围是（　　）

A．

（-2，1）

B．

（-1，2）

C．

（-∞，-1）∪（2，+∞）

D．

（-∞，-2）∪（1，+∞）

分析先得到函数f（x）在定义域上是增函数，再由函数单调性定义求解即可．

解答解：由分段函数可得当x≥0时f（x）=x²+4x=（x+2）²-4为增函数，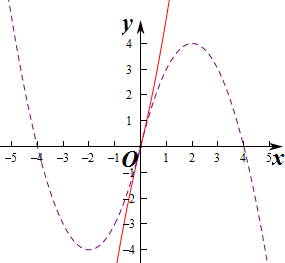
当x＜0时，f（x）=4x-x²=-（x-2）²+4为增函数，
∴f（x）在定义域上是增函数（如图）
若f（2-a²）＞f（a），
则2-a²＞a，即a²+a-2＜0
解得：-2＜a＜1
∴实数a的取值范围是（-2，1），
故选：A．

点评本题主要考查函数的单调性定义在解不等式中的应用，利用分段函数的表达式结合一元二次函数的性质是解决本题的关键．本题也可以直接利用数形结合进行判断．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

	A．	向左平移$\frac{π}{6}$个单位长度，再把所得图象各点的横坐标伸长到原来的2倍，纵坐标不变
	B．	向左平移$\frac{π}{6}$个单位长度，再把所得图象各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变
	C．	向左平移$\frac{π}{3}$个单位长度，再把所得图象各点的横坐标伸长到原来的2倍，纵坐标不变
	D．	向左平移$\frac{π}{3}$个单位长度，再把所得图象各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变

15．已知函数f（x）=e^x，g（x）=ax+b，其中a，b∈R．
（Ⅰ）若a=-1，函数y=$\frac{1}{f（x）+g（x）}$在（0，+∞）上有意义，求b的取值范围；
（Ⅱ）若0≤2a≤b≤1，求证：当x≥0时，$\frac{1}{f（x）}$+$\frac{x}{g（x）}$≥1．

12．已知函数f（x）是定义在R上的奇函数，且函数f（x）的图象关于直线x=1对称，当0≤x≤2时，f（x）=x²+bx，则f（2015）=1．

19．已知直线l，m，平面α，β，下列命题正确的是（　　）

	A．	l∥β，l?α⇒α∥β		B．	l∥β，m∥β，l?α，m?α⇒α∥β
	C．	l∥m，l?α，m?β⇒α∥β		D．	l∥β，m∥β，l?α，m?α，l∩m=M⇒α∥β

9．若复数z=（x²-1）+（x-1）i，（x∈R）为纯虚数，则|z|=2．

16．已知等差数列{a_n}满足，a₂+a₃+a₆+a₉+a₁₀=25，则a₅+a₇为（　　）

13．△ABC的顶点A（3，4），B（6，0），且∠A的内角平分线AT所在的直线方程为7x-y-17=0，则边AC所在的直线方程是（　　）

5．在等差数列{a_n}中，
①若a₃+a₁₂=60，a₆+a₇+a₈=75，求数列{a_n}的通项公式；
②已知a₂+a₃+a₄+a₅=34，a₂•a₅=52，求公差d．

试题分类