题目内容
【题目】在△ABC中,中线长AM=2.
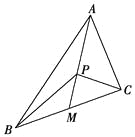
(1)若![]() =-2
=-2![]() ,求证:
,求证:![]() +
+![]() +
+![]() =0;
=0;
(2)若P为中线AM上的一个动点,求![]() ·(
·(![]() +
+![]() )的最小值.
)的最小值.
【答案】(1)见解析;(2)最小值-2.
【解析】
试题(1) ∵M是BC的中点,∴![]() =
=![]() (
(![]() +
+![]() ).代入
).代入![]() =-2
=-2![]() ,得
,得![]() =-
=-![]() -
-![]() ,即
,即![]() +
+![]() +
+![]() =0
=0
(2)若P为中线AM上的一个动点,若AM=2,我们易将![]() ·(
·(![]() +
+![]() ),转化为-2|
),转化为-2|![]() ||
||![]() |=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
|=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
试题解析:(1)证明:∵M是BC的中点,
∴![]() =
=![]() (
(![]() +
+![]() )
)
代入![]() =-2
=-2![]() ,得
,得![]() =-
=-![]() -
-![]() ,
,
即![]() +
+![]() +
+![]() =0
=0
(2)设|![]() |=x,则|
|=x,则|![]() |=2-x(0≤x≤2)
|=2-x(0≤x≤2)
∵M是BC的中点,∴![]() +
+![]() =2
=2![]()
∴![]() ·(
·(![]() +
+![]() )=2
)=2![]() ·
·![]() =-2|
=-2|![]() ||
||![]() |
|
=-2x(2-x)=2(x2-2x)=2(x-1)2-2,
当x=1时,取最小值-2

【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
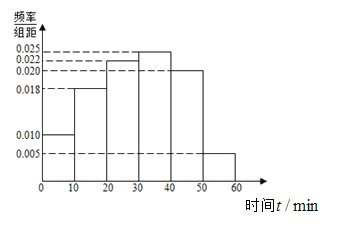
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.
(Ⅰ)根据已知条件完成下面![]() 列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
非体育健康A类学生 | 体育健康A类学生 | 合计 | |
男生 | |||
女生 | |||
合计 |
(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
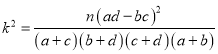
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|