Question

【题目】函数f(x)=Asin(wx+j)(A＞0，w＞0，-＜j＜，x∈R)的部分图象如图所示：，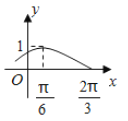

(1)求函数y=f(x)的解析式；(2)当x∈时，求f(x)的取值范围.

Answer 1

【答案】（1）f(x)=sin(x+)；（2）[-1,].

【解析】

试题（1）图像离平衡位置最高值为1可知A=1,又从图可看出周期的四分之一为，根据可求得w的值，对于j可通过代入(，1)点求得，但要注意j的范围；（2）本小题考查三角函数求值域问题，由x的范围可先求出x+的范围，结合正弦函数图像可求出sin(x+)的取值范围.

试题解析：(1)由图象得A=1，，所以T=2p，则w="1." 将点(，1)代入得sin(+j)=1，而-＜j＜，所以j=，因此函数f(x)=sin(x+).

(2)由于x∈，-≤x+≤，所以-1≤sin(x+)≤，所以f(x)的取值范围[-1,].