题目内容
从装有n+1个球（其中n个白球，1个黑球）的口袋中取出m个球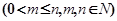
，
共有
种取法，在这种取法中，可以分为两类：一类是取出的m个球全部为白球，
另一类是取出的m个球中有1个黑球，共有
种取法，
即有等式：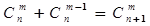
成立.试根据上述思想可得
(用组合数表示)
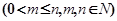，共有
种取法，在这种取法中，可以分为两类：一类是取出的m个球全部为白球，另一类是取出的m个球中有1个黑球，共有
种取法，即有等式：
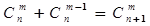成立.试根据上述思想可得 (用组合数表示)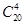 
在Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k中，
从第一项到最后一项分别表示：从装有n个白球，k个黑球的袋子里，
取出m个球的所有情况取法总数的和，故答案应为：从从装有n+k球中取出m个球的不同取法数Cn+km,本小题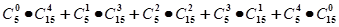
意思是从装有20（其中15白，5个黑）个球的口袋中取出4个球，共有的取法数为.
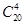从第一项到最后一项分别表示：从装有n个白球，k个黑球的袋子里，
取出m个球的所有情况取法总数的和，故答案应为：从从装有n+k球中取出m个球的不同取法数Cn+km,本小题
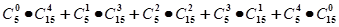意思是从装有20（其中15白，5个黑）个球的口袋中取出4个球，共有的取法数为.
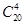练习册系列答案
步步高达标卷系列答案
相关题目
方格中的9个区域，要求每行每列的三个区域都不同色，则不同的填涂种数共有 
; 
; 
; 
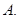
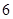
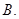
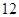
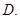
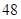
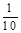
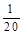
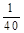
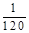
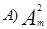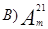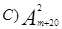