题目内容
(2012•云南模拟)选修4-5:不等式选讲
设函数f(x)=|2x+1|-|x-4|
(1)解不等式f(x)>2.
(2)求函数y=f(x)的最小值.
设函数f(x)=|2x+1|-|x-4|
(1)解不等式f(x)>2.
(2)求函数y=f(x)的最小值.
分析:将绝对值符号去掉,函数写成分段函数,再分段求出不等式的解集及函数的值域,即可确定不等式的解集及函数的最小值.
解答:解:函数f(x)=|2x+1|-|x-4|=
(1)令-x-5>2,则x<-7,∵x≤-
,∴x<-7
令3x-3>2,则x>
,∵-
<x<4,∴
<x<4
令x-5>2,则x>7,∵x≥4,∴x>7
∴f(x)>2的解集为:{x|x<-7或
<x<4或x>7}
(2)当x≤-
时,-x-5≥-
当-
<x<4时,-
<3x-3<9
当x≥4时,x-5≥-1
∴函数y=f(x)的最小值为-
.
|
(1)令-x-5>2,则x<-7,∵x≤-
| 1 |
| 2 |
令3x-3>2,则x>
| 5 |
| 3 |
| 1 |
| 2 |
| 5 |
| 3 |
令x-5>2,则x>7,∵x≥4,∴x>7
∴f(x)>2的解集为:{x|x<-7或
| 5 |
| 3 |
(2)当x≤-
| 1 |
| 2 |
| 9 |
| 2 |
当-
| 1 |
| 2 |
| 9 |
| 2 |
当x≥4时,x-5≥-1
∴函数y=f(x)的最小值为-
| 9 |
| 2 |
点评:本题考查绝对值函数,考查分类讨论的数学思想,考查函数的最值,属于中档题.

练习册系列答案
相关题目
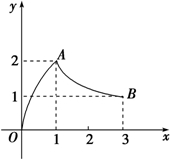 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(