题目内容
【题目】在![]() 中,AB=AC.试求出
中,AB=AC.试求出![]() 应满足的一个充分必要条件,使得在
应满足的一个充分必要条件,使得在![]() 的内部存在一个点
的内部存在一个点![]() ,满足(1)
,满足(1)![]() ;(2)
;(2)![]() .
.
【答案】见解析
【解析】
如图设以![]() 为半径,分别以
为半径,分别以![]() 、
、![]() 为圆心的两圆相交于另外一点
为圆心的两圆相交于另外一点![]() ,显然
,显然![]() 是等边三
是等边三
角形,且![]() ,
,![]() .
.
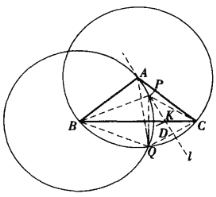
因为点![]() 在
在![]() 内,且
内,且![]() ,所以,点
,所以,点![]() 在弧
在弧![]() 上.
上.
又![]() ,从而,
,从而,![]() .故
.故![]() .
.
设弧![]() 交
交![]() 于点
于点![]() ,由以上的分析可知:
,由以上的分析可知:
在![]() 内部存在一点
内部存在一点![]() ,使得
,使得![]() 且
且![]() 的充分必要条件是,
的充分必要条件是,
线段![]() 的垂直平分线与弧
的垂直平分线与弧![]() 的内部(不包括点
的内部(不包括点![]() )有交点,
)有交点,
即等价于![]() 的角平分线
的角平分线![]() 交弧
交弧![]() 的内部于一点.
的内部于一点.
考虑两个极端情形:
(i)![]() 与
与![]() 重合.这时
重合.这时![]() ,
,
(ii)角平分线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() .这时由
.这时由![]() 及
及![]() 可得
可得![]() 与
与![]() 的夹角为
的夹角为![]() .
.
从而,![]() ,
,![]() .
.
再由上述充分必要条件可知:
点![]() 存在
存在
![]() 的角平分线
的角平分线![]() 交
交![]() 的内部于一点
的内部于一点
![]() (否则就不会有交点).
(否则就不会有交点).
因此所求的充分必要条件为![]() .
.
注:我们可证明![]() .
.
记![]() ,则
,则
![]() ,
,![]() ,
,![]()
所以,![]() .
.
于是,![]() 垂直平分线段
垂直平分线段![]() .
.
记![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
由![]() ,
,![]() 可知
可知
![]() .
.
又![]() ,
,
故![]() .
.
注:此题可利用“Femat点”求解,也可用“三角法”求解.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】某高校调查喜欢“统计”课程是否与性别有关,随机抽取了55个学生,得到统计数据如表:
喜欢 | 不喜欢 | 总计 | |
男生 | 20 | ||
女生 | 20 | ||
总计 | 30 | 55 |
(1)完成表格的数据;
(2)判断是否在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关?
参考公式:![]()
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 | 0.1 |
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).