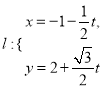题目内容
【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ,
,![]() ,
,![]() ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求?
【答案】模型![]() 确实能符合公司要求.
确实能符合公司要求.
【解析】
画出函数图像,根据图像得到模型![]() 进行奖励时才符合公司的要求,得到答案.
进行奖励时才符合公司的要求,得到答案.
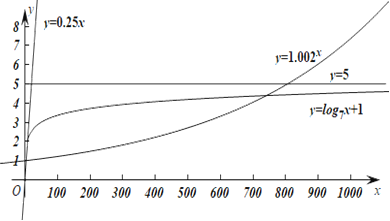
作出函数![]() ,
,![]() ,
,![]() ,
,![]() 的图像
的图像
观察图像发现,在区间![]() 上,模型
上,模型![]() ,
,![]() 的图像都有一部分在直线
的图像都有一部分在直线![]() 的上方,只有模型
的上方,只有模型![]() 的图像始终在
的图像始终在![]() 的下方,
的下方,
这说明只有按模型![]() 进行奖励时才符合公司的要求.下面通过计算确认上述判断.
进行奖励时才符合公司的要求.下面通过计算确认上述判断.
首先计算每个模型的奖金总数不超过5万元.
对于模型![]() ,它在区间
,它在区间![]() 上递增,而且当
上递增,而且当![]() 时,
时,![]() ,因此,当
,因此,当![]() 时,
时,![]() ,所以该模型不符合要求;
,所以该模型不符合要求;
对于模型![]() ,由函数图像,并利用计算器,可知在区间
,由函数图像,并利用计算器,可知在区间![]() 内有一个点
内有一个点![]() 满足
满足![]() ,由于它在区间
,由于它在区间![]() 上递增,因此当
上递增,因此当![]() 时,
时,![]() ,所以该模型也不符合要求;
,所以该模型也不符合要求;
对于模型![]() ,它在区间
,它在区间![]() 上递增,而且当
上递增,而且当![]() 时,
时,![]() ,所以它符合奖金总数不超过5万元的要求.
,所以它符合奖金总数不超过5万元的要求.
再计算按模型![]() 奖励时,奖金是否不超过利润的25%,即当
奖励时,奖金是否不超过利润的25%,即当![]() 时,是否有
时,是否有![]() 成立.
成立.
令![]() ,
,![]() .
.
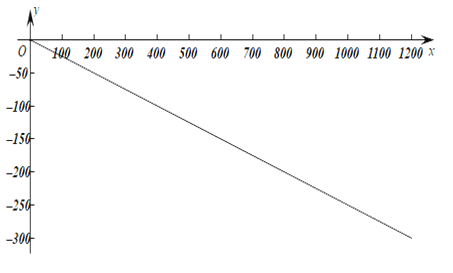
作出函数![]() 的图像,由图像可知它是递减的,
的图像,由图像可知它是递减的,
因此![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() .
.
说明按模型![]() 奖励,奖金不会超过利润的25%.
奖励,奖金不会超过利润的25%.
综上所述,模型![]() 确实能符合公司要求.
确实能符合公司要求.

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加![]() 现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 |
|
|
|
|
|
![]() Ⅰ
Ⅰ![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() Ⅱ
Ⅱ![]() 若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
![]() 参考公式:
参考公式: ,
,![]()