题目内容
【题目】已知等差数列{an}的公差d＞0，设{an}的前n项和为Sn ， a1=1，S2S3=36．
（1）求d及Sn；
（2）求m，k（m，k∈N*）的值，使得am+am+1+am+2+…+am+k=65．
【答案】
（1）解：由a1=1，S2S3=36得，
（a1+a2）（a1+a2+a3）=36，
即（2+d）（3+3d）=36，化为d2+3d﹣10=0，
解得d=2或﹣5，
又公差d＞0，则d=2，
所以Sn=n 
=n2（n∈N*）．
（2）解：由（1）得，an=1+2（n﹣1）=2n﹣1，
由am+am+1+am+2+…+am+k=65得， 
，
即（k+1）（2m+k﹣1）=65，
又m，k∈N*，则（k+1）（2m+k﹣1）=5×13，或（k+1）（2m+k﹣1）=1×65，
下面分类求解：
当k+1=5时，2m+k﹣1=13，解得k=4，m=5；
当k+1=13时，2m+k﹣1=5，解得k=12，m=﹣3，故舍去；
当k+1=1时，2m+k﹣1=65，解得k=0，故舍去；
当k+1=65时，2m+k﹣1=1，解得k=64，m=﹣31，故舍去；
综上得，k=4，m=5．
【解析】（1）根据等差数列通项公式和前n项和公式，把条件转化为关于公差d的二次方程求解，注意d的范围对方程的根进行取舍；（2）由（1）求出等差数列{an}的通项公式，利用等差数列的前n项和公式，对am+am+1+am+2+…+am+k=65化简，列出关于m、k的方程，再由m，k∈N*进行分类讨论，求出符合条件的m、k的值．
【考点精析】关于本题考查的等差数列的前n项和公式和数列的前n项和，需要了解前n项和公式：
；数列{an}的前n项和sn与通项an的关系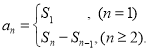
才能得出正确答案．
练习册系列答案
相关题目
