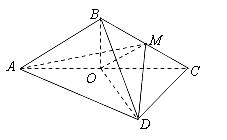
题目内容
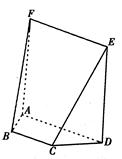
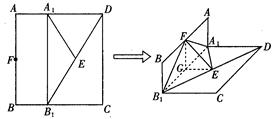
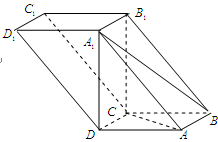
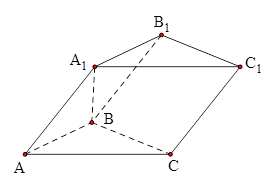
如图,在直四棱柱 中,已知
中,已知 ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)设 是
是 上一点,试确定
上一点,试确定 的位置,使
的位置,使 平面
平面 ,并说明理由.
,并说明理由.
(Ⅰ)先证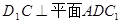 (Ⅱ)
(Ⅱ) 是
是 的中点
的中点
解析试题分析:(Ⅰ)证明:在直四棱柱 中,连结
中,连结 ,
, 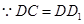 ,
,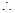 四边形
四边形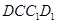 是正方形.
是正方形. 
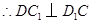 .又
.又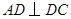 ,
,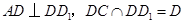 ,
,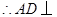 平面
平面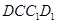 ,又
,又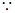
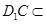 平面
平面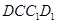 ,
, .
.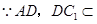 平面
平面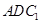 ,
,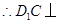 平面
平面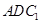 ,又
,又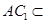 平面
平面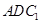 ,
, .
.
(2)连结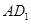 ,连结
,连结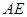 ,
,
设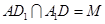 ,
, ,连结
,连结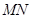 ,
,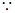 平面
平面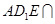 平面
平面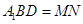 ,要使
,要使 平面
平面 ,
,
须使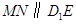 , 又
, 又 是
是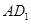 的中点.
的中点. 是
是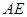 的中点.又易知
的中点.又易知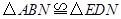 ,
,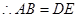 .
.
即 是
是 的中点.综上所述,当
的中点.综上所述,当 是
是 的中点时,可使
的中点时,可使 平面
平面 .
.
考点:线线垂直 线面平行
点评:熟练掌握线面平行、垂直的判定定理和性质定理是解题的关键,属中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
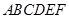 中,四边形
中,四边形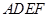 是正方形,
是正方形,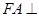 平面
平面 ∥
∥
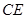 与
与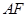 所成角的余弦值;
所成角的余弦值;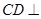 平面
平面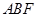 ;
; 的正切值。
的正切值。 中,平面
中,平面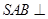 平面
平面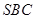 ,
,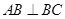 ,
,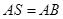 . 过点
. 过点 作
作 ,垂足为
,垂足为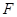 ,点
,点 ,
, 分别为棱
分别为棱 ,
,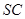 的中点.
的中点.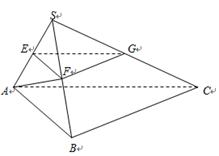
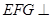 平面
平面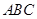 ;
;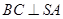 .
. 的边长为6,
的边长为6, ,
,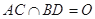 .将菱形
.将菱形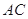 折起,得到三棱锥 ,点
折起,得到三棱锥 ,点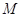 是棱
是棱 的中点,
的中点,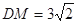 .
.
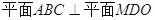 ;
; 的体积.
的体积.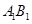 折成直角二面角,且
折成直角二面角,且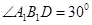 .
.
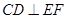
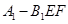 的体积.
的体积.
 中,
中, 平面
平面 ,底面
,底面 ,
,
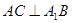 ;
;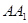 上存在一点
上存在一点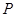 ,使得
,使得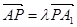 ,
,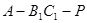 的大小为
的大小为 时,求实数
时,求实数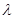 的值.
的值.
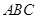 —
— ,侧面
,侧面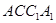 与底面
与底面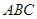 垂直,∠
垂直,∠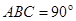 ,
,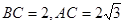 ,且
,且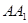 ⊥
⊥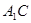 ,
,
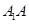 与平面
与平面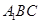 是否垂直,并说明理由;
是否垂直,并说明理由;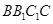 与底面
与底面