Question

【题目】如图,在矩形中, , 为的中点, 为的中点.将沿折起到,使得平面平面（如图）.

图1 图2

（Ⅰ）求证: ；

（Ⅱ）求直线与平面所成角的正弦值；

（Ⅲ）在线段上是否存在点,使得平面?若存在,求出的值;若不存在,请说明理由.

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ） ；（Ⅲ） .

【解析】试题分析：（Ⅰ）根据等腰三角形的性质可得,由平面平面可得平面,从而可得；（Ⅱ）取中点为,连结，由矩形性质, ,可知，由（Ⅰ）可知, ，以为原点, 为轴, 为轴, 为轴建立坐标系，求出平面的一个法向量及直线的方向向量，利用空间向量夹角余弦公式可得结果；（Ⅲ）假设在线段上存在点,满足平面，设，利用直线与平面的法向量垂直，数量积为零，列方程求解即可.

.

试题解析：（Ⅰ）如图,在矩形中,

, 为中点, ,

为的中点,

由题意可知, ,

平面平面

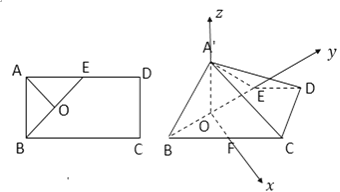
图1 图2

平面平面,平面，

平面，

平面,

，

（Ⅱ）取中点为,连结，

由矩形性质, ,可知，

由（Ⅰ）可知, ，

以为原点, 为轴, 为轴, 为轴建立坐标系，

在中,由,则,

所以

,,

设平面的一个法向量为，

则,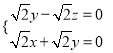令,则，

所以，

设直线与平面所成角为，

，

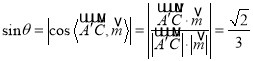所以直线与平面所成角的正弦值为.

（Ⅲ）假设在线段上存在点,满足平面

设，

由,,所以，

,，

若平面,则，

所以,解得，

所以.

【方法点晴】本题主要考查面面垂直的性质以及利用空间向量求线面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.