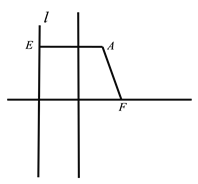
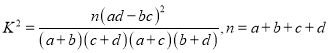题目内容
【题目】已知平面内的定点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() ,动圆
,动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .在曲线
.在曲线![]() 上任取一点
上任取一点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
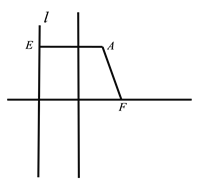
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)判断![]() 的平分线所在的直线与曲线的交点个数,并说明理由.
的平分线所在的直线与曲线的交点个数,并说明理由.
【答案】(1)![]() (2)见解析. (3)见解析.
(2)见解析. (3)见解析.
【解析】试题分析; (1)以FK的中点为坐标原点O,FK所在的直线为x轴,过O的垂线为y轴建立直角坐标系,求得F的坐标和直线l的方程,运用抛物线的定义,可得M的轨迹和方程;(2)利用向量点积运算可得到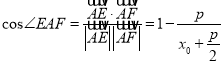 ,根据条件
,根据条件![]() ,可得到角的范围;(3)∠EAF的平分线所在的直线与曲线的交点个数为1.设A(x0,y0),可得y02=2px0,讨论当A与O重合时,显然一个交点;当A不与O重合,A在上方,推得四边形EAFM为菱形,求得AMF的正切值,设出直线AM的方程,联立抛物线的方程,即可得到证明.
,可得到角的范围;(3)∠EAF的平分线所在的直线与曲线的交点个数为1.设A(x0,y0),可得y02=2px0,讨论当A与O重合时,显然一个交点;当A不与O重合,A在上方,推得四边形EAFM为菱形,求得AMF的正切值,设出直线AM的方程,联立抛物线的方程,即可得到证明.
解析:
(1)过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴, ![]() 轴与直线
轴与直线![]() 的交点为
的交点为![]() 点,以
点,以![]() 的中点为原点建立直角坐标系.
的中点为原点建立直角坐标系.
设![]()
![]() ,
, ![]() 到定点
到定点![]() 与到定直线
与到定直线![]() 的距离相等,
的距离相等,
![]()
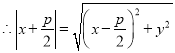
化简得: ![]()
(2)设![]()
![]()
![]()

![]() ,
, ![]() ,
,![]()
![]()
![]() .
.
(3)设![]()
![]() ,
, ![]() .
.
由![]() ,得
,得![]() 的平分线所在的直线方程就是
的平分线所在的直线方程就是![]() 边
边![]() 上的高所在的直线方程.
上的高所在的直线方程.
![]()
![]() 的平分线所在的直线方程为
的平分线所在的直线方程为![]() .
.
由![]() ,消
,消![]() 得
得![]() .
.
![]()
![]() ,
, ![]()
![]() .
.
![]()
![]() 的平分线所在的直线与曲线有且只有一个交点.
的平分线所在的直线与曲线有且只有一个交点.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】进入高三,同学们的学习越来越紧张,学生休息和锻炼的时间也减少了.学校为了提高学生的学习效率,鼓励学生加强体育锻炼.某中学高三(3)班有学生50人.现调查该班学生每周平均体育锻炼时间的情况,得到如下频率分布直方图.其中数据的分组区间为: ![]()

(1)求学生周平均体育锻炼时间的中位数(保留3位有效数字);
(2)从每周平均体育锻炼时间在 ![]() 的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
(3)现全班学生中有40%是女生,其中3个女生的每周平均体育锻炼时间不超过4小时.若每周平均体育锻炼时间超过4小时称为经常锻炼,问:有没有90%的把握说明,经常锻炼与否与性别有关?
附: 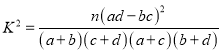
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某出租车公司购买了140辆纯电动汽车作为运营车辆,目前我国纯电动汽车按续航里程数R(单位:千米)分为3类,即A类:![]() ,B类:
,B类:![]() ,C类:
,C类:![]() .该公司对这140辆车的行驶总里程进行统计,结果如下表:
.该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 | A类 | B类 | C类 |
已行驶总里程不超过10万千米的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万千米的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万千米的概率;
(2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从C类车中抽取了n辆车.
①求n的值;
②如果从这n辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万千米的概率.
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中