题目内容
设函数f(x)=log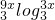 ,且
,且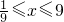
(1)求f(3)的值;
(2)若令t=log3x,求t取值范围;
(3)将f(x)表示成以t(t=log3x)为自变量的函数,并由此,求函数f(x)的最大值与最小值及与之对应的x的值.
解:(1)f(3)=log327•log39=3×2=6;
(2)t=log3x,又∵ ≤x≤9,
≤x≤9,
∴-2≤log3x≤2,
∴-2≤t≤2即t的取值范围为[-2,2];
(3)由f(x)=(log3x+2)(log3x+1)=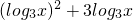 +2=t2+3t+2,
+2=t2+3t+2,
令g(t)=t2+3t+2=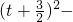
 ,t∈[-2,2],
,t∈[-2,2],
①当t=- 时,g(t)min=-
时,g(t)min=- ,即log3x=-
,即log3x=- ,解得
,解得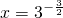 =
= ,
,
f(x)min=- ,此时
,此时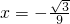 ;
;
②当t=2时,g(t)max=g(2)=12,即log3x=2?x=9,
∴f(x)max=12,此时x=9;
分析:(1)根据对数的运算法则即可求得;
(2)由对数运算性质及 ≤x≤9,即可求得t的范围;
≤x≤9,即可求得t的范围;
(3)根据对数运算法则可把f(x)转化为关于t的二次函数,利用二次函数的性质可求得其最值,通过解对数方程可解得相应x的值;
点评:本题考查对数的运算法则、函数求值及二次函数性质,考查转化思想,解决本题的关键是掌握对数的运算法则.
(2)t=log3x,又∵
 ≤x≤9,
≤x≤9,∴-2≤log3x≤2,
∴-2≤t≤2即t的取值范围为[-2,2];
(3)由f(x)=(log3x+2)(log3x+1)=
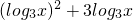 +2=t2+3t+2,
+2=t2+3t+2,令g(t)=t2+3t+2=
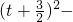
 ,t∈[-2,2],
,t∈[-2,2],①当t=-
 时,g(t)min=-
时,g(t)min=- ,即log3x=-
,即log3x=- ,解得
,解得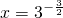 =
= ,
,f(x)min=-
 ,此时
,此时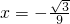 ;
;②当t=2时,g(t)max=g(2)=12,即log3x=2?x=9,
∴f(x)max=12,此时x=9;
分析:(1)根据对数的运算法则即可求得;
(2)由对数运算性质及
 ≤x≤9,即可求得t的范围;
≤x≤9,即可求得t的范围;(3)根据对数运算法则可把f(x)转化为关于t的二次函数,利用二次函数的性质可求得其最值,通过解对数方程可解得相应x的值;
点评:本题考查对数的运算法则、函数求值及二次函数性质,考查转化思想,解决本题的关键是掌握对数的运算法则.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目