题目内容
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 曲线
曲线![]() 与
与![]() 轴交于不同的两点;
轴交于不同的两点;
若![]() 为假命题,
为假命题, ![]() 为真命题,求
为真命题,求![]() 的取值范围.
的取值范围.
【答案】![]() 或
或![]() 或
或![]()
【解析】试题分析:首先根据已知条件并结合换元法和二次函数在区间上的最值以及一元二次方程根的情况分别求出命题![]() ,
, ![]() 为真命题时所满足的
为真命题时所满足的![]() 的取值范围,然后根据已知条件可知命题
的取值范围,然后根据已知条件可知命题![]() ,
, ![]() 中一个为真命题,一个为假命题,并利用补集的思想求出
中一个为真命题,一个为假命题,并利用补集的思想求出![]() 的取值范围.
的取值范围.
试题解析:若p为真,则由于![]() 为
为![]() 的局部奇函数,从而
的局部奇函数,从而![]() ,即
,即![]() 在
在![]() 上有解,令
上有解,令![]() ,则
,则![]() ,又
,又![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,从而
上递增,从而![]() ,得
,得![]() ,故有
,故有![]() . 若
. 若![]() 为真,则有
为真,则有![]() ,得
,得![]() 或
或![]() . 又由“
. 又由“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,则
”为真命题,则![]() 与
与![]() 一真一假;若
一真一假;若![]() 真
真![]() 假,则
假,则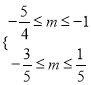 ,得无交集;若
,得无交集;若![]() 假
假![]() 真,则
真,则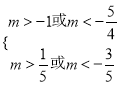 ,得
,得![]() 或
或![]() 或
或![]() ,综上知
,综上知![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目