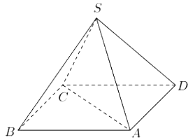
题目内容
【题目】已知椭圆![]() 的右焦点
的右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,原点到过点
的焦点重合,原点到过点![]() ,
,![]() 的直线的距离是
的直线的距离是![]() .
.
![]() 1
1![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 2
2![]() 设动直线
设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,过
,过![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 在定直线上,并求出定直线的方程.
在定直线上,并求出定直线的方程.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() .
.
【解析】
![]() 1
1![]() 由抛物线的焦点坐标求得
由抛物线的焦点坐标求得![]() ,结合隐含条件得到
,结合隐含条件得到![]() ,再由点到直线的距离公式得到关于a,b的另一关系式,联立方程组求得a,b的值,则椭圆方程可求;
,再由点到直线的距离公式得到关于a,b的另一关系式,联立方程组求得a,b的值,则椭圆方程可求;![]() 2
2![]() 联立直线方程和椭圆方程,消去y得到
联立直线方程和椭圆方程,消去y得到![]() ,由判别式等于0整理得到
,由判别式等于0整理得到![]() ,代入
,代入![]() 求得P的坐标,然后写出直线
求得P的坐标,然后写出直线![]() 方程为
方程为![]() ,联立方程组
,联立方程组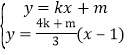 ,求得
,求得![]() ,即说明点Q在定直线
,即说明点Q在定直线![]() 上.
上.
![]() 1
1![]() 由抛物线的焦点坐标为
由抛物线的焦点坐标为![]() ,得
,得![]() ,
,
因此![]() ,
,
直线AB:![]() ,即
,即![]() .
.
![]() 原点O到直线AB的距离为
原点O到直线AB的距离为![]()
![]() ,
,
联立![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]() 椭圆C的方程为
椭圆C的方程为![]() ;
;
![]() 2
2![]() 由
由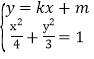 ,得方程
,得方程![]() ,
,![]()
由直线与椭圆相切,得![]() 且
且![]() ,
,
整理得:![]() ,
,
将![]() ,即
,即![]() 代入
代入![]() 式,得
式,得![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() ,
,
又![]() ,
,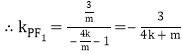 ,则
,则![]() ,
,
![]() 直线
直线![]() 方程为
方程为![]() ,
,
联立方程组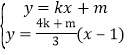 ,得
,得![]() ,
,
![]() 点Q在定直线
点Q在定直线![]() 上.
上.

 名校课堂系列答案
名校课堂系列答案【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
广告收入y(千万元) | 2 | 2.2 | 2.5 | 2.8 | 3 | 2.5 | 2.3 | 2 | 1.8 |
根据这9年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.243;根据后5年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.984.
(Ⅰ)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测;方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:
相关性检验的临界值表:
n-2 | 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(Ⅱ)某购物网站同时销售某本畅销书籍的纸质版本和电子书,某班级有五名同学在该网站购买了这本书,其中三人只购买了电子书,另两人只购买了纸质书,从这五人中任取两人,求两人都购买了电子书的概率.