题目内容
如图所示,在正三棱柱ABC-A1B1C1中,AB=1.若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( ).

A. 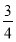 B.
B.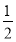 C.
C.  D.1
D.1
A
【解析】取AB中点D,连接CD,C1D,则∠CDC1是二面角C-AB-C1的平面角.
因为AB=1,所以CD=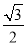 ,
,
所以在Rt△DCC1中,CC1=CD·tan 60°=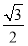 ×
×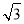 =
=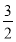 ,C1D=
,C1D=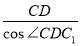 =
=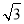 .
.
设点C到平面C1AB的距离为h,
由VC-C1AB=VC1-ABC,得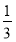 ×
×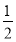 ×1×
×1×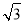 h=
h=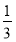 ×
×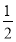 ×1×
×1×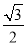 ×
×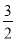 ,
,
解得h=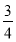 .故选A
.故选A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下表:
| 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:

K2=
A.估计该地区老年人中,需要志愿者提供帮助的老年人的比例为10%
B.估计该地区老年人中,需要志愿者提供帮助的老年人的比例为20%
C.有99%的把握认为该地区的老年人需要志愿者提供帮助与性别有关
D.有99%的把握认为该地区的老年人需要志愿者提供帮助与性别无关