题目内容

若函数f（x）=kax-a-x（a＞0且a≠1）在（-∞，+∞）上既是奇函数又是增函数，则其导函数f′（x）的图象可能是（　　）
分析：由奇函数和增函数的性质可得k=1，a＞1，进而可得函数的解析式，求导后综合研究选项可得答案．
解答：解：∵函数f（x）=kax-a-x，（a＞0且a≠1）在（-∞，+∞）上是奇函数
则f（-x）+f（x）=0，即ka-x-ax+kax-a-x=0，故（k-1）（ax-a-x）=0，解得k=1，
又∵函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上是增函数，所以a＞1，
因此函数f（x）=ax-a-x，（a＞1），求其导数可得f′（x）=（ax+a-x）lna，
可知f′（0）=2lna＞0，而四个选项中仅有B满足，
故选B
点评：本题考查函数的奇偶性和单调性，涉及导数和函数的图象，属中档题．
练习册系列答案
相关题目
对于具有相同定义域D的函数f（x）和g（x），若存在函数h（x）=kx+b（k，b为常数）对任给的正数m，
存在相应的x0∈D使得当x∈D且x＞x0时，总有
0＜f(x)-h(x)＜m
0＜h(x)-g(x)＜m
，则称直线l：y=ka+b为曲线y=f（x）和y=g（x）的“分渐进性”．给出定义域均为D={x|x＞1}的四组函数如下：
①f（x）=x2，g（x）=
x
②f（x）=10-x+2，g（x）=
2x-3
x
③f（x）=
x2+1
x
，g（x）=
xlnx+1
lnx
④f（x）=
2x2
x+1
，g（x）=2（x-1-e-x）
其中，曲线y=f（x）和y=g（x）存在“分渐近线”的是（　　）
A、①④B、②③C、②④D、③④
集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
（1）当k=
1
2
时，判断函数f（x）=
x
是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
（2）当k=
1
2
0时，若函数f（x）=
x
+t∈C∩D，求实数t的取值范围；
（3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．
函数f（x）=ka﹣x（k，a为常数，a＞0且a≠1）的图象过点A（0，1），B（3，8）．
（1）求函数f（x）的解析式；
（2）若函数，试判断函数g（x）的奇偶性．
集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
（1）当k=
1
2
时，判断函数f（x）=
x
是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
（2）当k=
1
2
0时，若函数f（x）=
x
+t∈C∩D，求实数t的取值范围；
（3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．
集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
（1）当k=时，判断函数f（x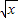）=是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
（2）当k=0时，若函数f（x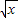）=+t∈C∩D，求实数t的取值范围；
（3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网