题目内容
集合C={f(x)|f(x)是在其定义域上的单调增函数或单调减函数},集合D={f(x)|f(x)在定义域内存在区间[a,b],使得f(x)在a,b上的值域是[ka,kb],k为常数}.(1)当k=
 时,判断函数f(x)=
时,判断函数f(x)=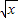 是否属于集合C∩D?并说明理由.若是,则求出区间[a,b];
是否属于集合C∩D?并说明理由.若是,则求出区间[a,b];(2)当k=
 0时,若函数f(x)=
0时,若函数f(x)=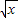 +t∈C∩D,求实数t的取值范围;
+t∈C∩D,求实数t的取值范围;(3)当k=1时,是否存在实数m,当a+b≤2时,使函数f(x)=x2-2x+m∈D,若存在,求出m的范围,若不存在,说明理由.
【答案】分析:(1)y= 的定义域是[0,+∞),在[0,+∞)上是单调增函数,设y=
的定义域是[0,+∞),在[0,+∞)上是单调增函数,设y= 在[a,b]的值域是[
在[a,b]的值域是[ ,
, ],能求出区间是[a,b].
],能求出区间是[a,b].
(2)设g(x)= +t,则g(x)是定义域[0,+∞)上的增函数,由g(x)∈C∩D,知存在区间[a,b]?[0,+∞),满足g(a)=
+t,则g(x)是定义域[0,+∞)上的增函数,由g(x)∈C∩D,知存在区间[a,b]?[0,+∞),满足g(a)= ,g(b)=
,g(b)= ,由此能求出实数t的取值范围.
,由此能求出实数t的取值范围.
(3)由f(x)=x2-2x+m∈D,且k=1,知当a<b≤1时,f(x)在[a,b]上单调递减,由此能推导出m的范围.
解答:解:(1)y= 的定义域是[0,+∞),
的定义域是[0,+∞),
∵y= 在[0,+∞)上是单调增函数,
在[0,+∞)上是单调增函数,
设y= 在[a,b]的值域是[
在[a,b]的值域是[ ,
, ],
],
由 ,解得
,解得 ,
,
故函数y= 属于集合C∩D,且这个区间是[0,4].
属于集合C∩D,且这个区间是[0,4].
(2)设g(x)= +t,则g(x)是定义域[0,+∞)上的增函数,
+t,则g(x)是定义域[0,+∞)上的增函数,
∵g(x)∈C∩D,∴存在区间[a,b]?[0,+∞),满足g(a)= ,g(b)=
,g(b)= ,
,
∴方程g(x)= 在[0,+∞)内有两个不等实根,
在[0,+∞)内有两个不等实根,
方程 +t=
+t= 在[0,+∞)内有两个不等实根,
在[0,+∞)内有两个不等实根,
令 ,则其化为m+t=
,则其化为m+t= ,
,
即m2-2m-2t=0有两个非负的不等实根,
∴ ,解得-
,解得- .
.
(3)f(x)=x2-2x+m∈D,且k=1,
∴当a<b≤1时,f(x)在[a,b]上单调递减,
 ,
,
两式相减,得a+b=1,
∴ ,
,
 ,
,
∴方程0=m-1-x+x2在x≤1上有两个不同的解,
解得m∈[1, ).
).
点评:本题考查二次函数的性质的应用,综合性强,难度大,对数学思维的要求较高,有一定的探索性.解题时要认真审题,注意等价转化思想的合理运用.
 的定义域是[0,+∞),在[0,+∞)上是单调增函数,设y=
的定义域是[0,+∞),在[0,+∞)上是单调增函数,设y= 在[a,b]的值域是[
在[a,b]的值域是[ ,
, ],能求出区间是[a,b].
],能求出区间是[a,b].(2)设g(x)=
 +t,则g(x)是定义域[0,+∞)上的增函数,由g(x)∈C∩D,知存在区间[a,b]?[0,+∞),满足g(a)=
+t,则g(x)是定义域[0,+∞)上的增函数,由g(x)∈C∩D,知存在区间[a,b]?[0,+∞),满足g(a)= ,g(b)=
,g(b)= ,由此能求出实数t的取值范围.
,由此能求出实数t的取值范围.(3)由f(x)=x2-2x+m∈D,且k=1,知当a<b≤1时,f(x)在[a,b]上单调递减,由此能推导出m的范围.
解答:解:(1)y=
 的定义域是[0,+∞),
的定义域是[0,+∞),∵y=
 在[0,+∞)上是单调增函数,
在[0,+∞)上是单调增函数,设y=
 在[a,b]的值域是[
在[a,b]的值域是[ ,
, ],
],由
 ,解得
,解得 ,
,故函数y=
 属于集合C∩D,且这个区间是[0,4].
属于集合C∩D,且这个区间是[0,4].(2)设g(x)=
 +t,则g(x)是定义域[0,+∞)上的增函数,
+t,则g(x)是定义域[0,+∞)上的增函数,∵g(x)∈C∩D,∴存在区间[a,b]?[0,+∞),满足g(a)=
 ,g(b)=
,g(b)= ,
,∴方程g(x)=
 在[0,+∞)内有两个不等实根,
在[0,+∞)内有两个不等实根,方程
 +t=
+t= 在[0,+∞)内有两个不等实根,
在[0,+∞)内有两个不等实根,令
 ,则其化为m+t=
,则其化为m+t= ,
,即m2-2m-2t=0有两个非负的不等实根,
∴
 ,解得-
,解得- .
.(3)f(x)=x2-2x+m∈D,且k=1,
∴当a<b≤1时,f(x)在[a,b]上单调递减,
 ,
,两式相减,得a+b=1,
∴
 ,
, ,
,∴方程0=m-1-x+x2在x≤1上有两个不同的解,
解得m∈[1,
 ).
).点评:本题考查二次函数的性质的应用,综合性强,难度大,对数学思维的要求较高,有一定的探索性.解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目