题目内容
【题目】已知椭圆C: ![]() =1(a>b>0),椭圆C的右焦点F的坐标为
=1(a>b>0),椭圆C的右焦点F的坐标为 ![]() ,短轴长为2.
,短轴长为2.
(I)求椭圆C的方程;
(II)若点P为直线x=4上的一个动点,A,B为椭圆的左、右顶点,直线AP,BP分别与椭圆C的另一个交点分别为M,N,求证:直线MN恒过点E(1,0).
【答案】解:(I)由题意可得c= ![]() ,2b=2,b=1,a2=b2+c2=4,
,2b=2,b=1,a2=b2+c2=4,
则a2=4,
∴椭圆C的方程为 ![]() .
.
(II)由 ![]() 可得椭圆的左、右顶点为A(﹣2,0),B(2,0).
可得椭圆的左、右顶点为A(﹣2,0),B(2,0).
设P(4,m),M(x1 , y1),N(x2 , y2),则直线 ![]() ,直线
,直线 ![]()
由 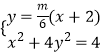 ,整理得:
,整理得: ![]() ,解得
,解得 ![]() ,
, ![]()
由 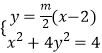 ,整理得:m2(x+2)2=4﹣x2 , 解得
,整理得:m2(x+2)2=4﹣x2 , 解得 ![]() ,
, ![]() ,
,![]() ,
, ![]() ,kME=kNE ,
,kME=kNE ,
M,N,E三点共线,即直线MN恒过点E(1,0).
另法:
由 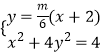 可得
可得 ![]() ,解得
,解得 ![]() ,
,
由 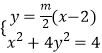 可得m2(x﹣2)2=4﹣x2 , 解得
可得m2(x﹣2)2=4﹣x2 , 解得 ![]() ,
,
所以 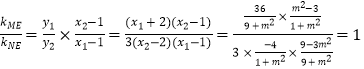
所以M,N,E三点共线,即直线MN恒过点E(1,0).
【解析】(I)由题意可知c= ![]() ,b=1,a2=b2+c2=4,即可求得椭圆方程;(II)由题意求得AP及BP的方程,分别代入椭圆方程,求得M和N点坐标,根据直线的斜率公式,可得kME=kNE , 则M,N,E三点共线,即直线MN恒过点E(1,0);
,b=1,a2=b2+c2=4,即可求得椭圆方程;(II)由题意求得AP及BP的方程,分别代入椭圆方程,求得M和N点坐标,根据直线的斜率公式,可得kME=kNE , 则M,N,E三点共线,即直线MN恒过点E(1,0);

练习册系列答案
相关题目