题目内容
【题目】已知x,y∈[0,π],则cos(x+y)+cosx+2cosy的最小值为 .
【答案】﹣2.25
【解析】解:令S=cos(x+y)+cosx+2cosy=cosxcosy﹣sinxsiny+cosx+2cosy
=cosx+(cosx+2)cosy﹣sinxsiny
=cosx﹣ ![]() θ)
θ)
∴S≥cosx﹣ ![]()
令:t= ![]() ,3≥t≥1,则cosx=
,3≥t≥1,则cosx= ![]()
故S≥ ![]() ﹣t=
﹣t= ![]() ,(3≥t≥1)
,(3≥t≥1)
当t=2时,S取得最小值为: ![]() .
.
∴即cos(x+y)+cosx+2cosy的最小值为: ![]() .
.
所以答案是:﹣2.25.
【考点精析】本题主要考查了两角和与差的余弦公式和三角函数的最值的相关知识点,需要掌握两角和与差的余弦公式:![]() ;函数
;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
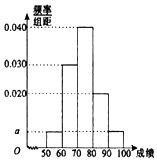
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如下表所示),规定80分及以上者晋级成功,否则晋级失败.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |