题目内容
 如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于
如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于分析:要求圆O的面积,关键是求圆的半径R,求半径有如下方法:构造含半径R的三角形,解三角形求出半径R值;或是根据正弦定理,
=
=
=2R,求出圆的半径后,代入圆的面积公式即可求解.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答:解:法一:连接OA、OB,则∠AOB=90°,
∵AB=4,
OA=OB,
∴R=OA=2
,
则S圆=π×(2
)2=8π;
法二:
2R=
=4
?R=2
,
则S圆=π×(2
)2=8π
∵AB=4,
OA=OB,
∴R=OA=2
| 2 |
则S圆=π×(2
| 2 |
法二:
2R=
| 4 |
| sin450 |
| 2 |
| 2 |
则S圆=π×(2
| 2 |
点评:求圆的半径有如下方法:①构造含半径R的三角形,解三角形求出半径R值;②如果圆为△ABC的外接圆,则根据正弦定理,
=
=
=2R;③如果圆为△ABC的内切圆,则根据面积公式S=
•l•r(其中l表示三角形的周长).
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 1 |
| 2 |

练习册系列答案
相关题目
 15、选做题:如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于
15、选做题:如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于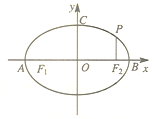 如图,点A,B,C是椭圆M:
如图,点A,B,C是椭圆M: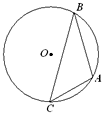 如图,点A,B,C是圆O上的点,且
如图,点A,B,C是圆O上的点,且 A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=
A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=