题目内容
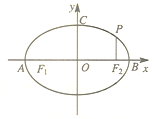 如图,点A,B,C是椭圆M:
如图,点A,B,C是椭圆M:| x2 |
| a2 |
| y2 |
| b2 |
①存在a,b使得△AF2P为等腰直角三角形
②存在a,b使得△F1F2P为等腰直角三角形
③存在a,b使得△OF2P为等腰直角三角形
④存在a,b使得△BF2P为等腰直角三角形
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
分析:利用椭圆的长轴,短轴,焦距的数量关系判定①②的正误;利用F2P与c的关系判定③④的正误,得到选项.
解答: 解:由题意可知F2P<b<a,所以存在a,b使得△AF2P为等腰直角三角形不可能,①是错误的;
解:由题意可知F2P<b<a,所以存在a,b使得△AF2P为等腰直角三角形不可能,①是错误的;
当2c=F2P时,即满足2c=
,a=(1+
)c时,△F1F2P为等腰直角三角形,所以②正确.
存在a,b使得△OF2P为等腰直角三角形,只需c=F2P即可,所以③正确.
只需BF2=F2P,即a-c=F2P可得出a=c,而a>c矛盾,所以④不正确.
故选C.
 解:由题意可知F2P<b<a,所以存在a,b使得△AF2P为等腰直角三角形不可能,①是错误的;
解:由题意可知F2P<b<a,所以存在a,b使得△AF2P为等腰直角三角形不可能,①是错误的;当2c=F2P时,即满足2c=
| b2 |
| a |
| 2 |
存在a,b使得△OF2P为等腰直角三角形,只需c=F2P即可,所以③正确.
只需BF2=F2P,即a-c=F2P可得出a=c,而a>c矛盾,所以④不正确.
故选C.
点评:本题考查题意的基本性质,长轴、短轴、焦距、通经之间的关系,考查学生的计算能力.

练习册系列答案
相关题目
 如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于
如图,点A,B,C是圆O上的点,且AB=4,∠ACB=45°,则圆O的面积等于 15、选做题:如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于
15、选做题:如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于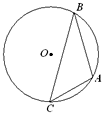 如图,点A,B,C是圆O上的点,且
如图,点A,B,C是圆O上的点,且 A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=
A:(坐标系与参数方程选做题)在极坐标系中,由θ=0,θ=