题目内容

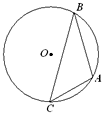如图，点A，B，C是圆O上的点，且BC=2
3
，∠BAC=
2π
3
，则圆O的面积等于
4π
4π
．
分析：设圆的半径为R，由正弦定理可得，
BC
sin∠BAC
=2R可求圆的半径，进而可求圆的面积
解答：解：设圆的半径为R
由正弦定理可得，
BC
sin∠BAC
=2R
∵BC=2
3
，∠BAC=
2π
3

∴2R=
2
3
sin
2π
3
=4
∴R=2，S=4π
故答案为：4π
点评：本题主要考查了正弦定理的简单应用，属于基础试题
练习册系列答案
相关题目
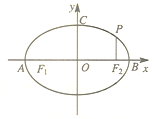精英家教网如图，点A，B，C是圆O上的点，且AB=4，∠ACB=45°，则圆O的面积等于
 
．
15、选做题：如图，点A、B、C是圆O上的点，且AB=4，∠ACB=30°，则圆O的面积等于
16π
．
精英家教网如图，点A，B，C是椭圆M：
x2
a2
+
y2
b2
=1的三个顶点，F1，F2是它的左、右焦点，P是M上一点，且PF2⊥OB．则下列命题：
①存在a，b使得△AF2P为等腰直角三角形
②存在a，b使得△F1F2P为等腰直角三角形
③存在a，b使得△OF2P为等腰直角三角形
④存在a，b使得△BF2P为等腰直角三角形
其中真命题的个数是（　　）
A、1B、2C、3D、4
A：（坐标系与参数方程选做题）在极坐标系中，由θ=0，θ=
π
3
，ρcosθ+ρsinθ=1围成图形的面积是
3-
3
4
3-
3
4
．
B：（几何证明选讲选做题）如图，点A，B，C是圆O上的点，且AB=4，∠ACB=30°，则圆O的面积等于
16π
16π
．
C：（不等式选讲）要使关于x的不等式|x-1|+|x-1|≤3在实数范围内有解，则a的取值范围是
[-2，4]
[-2，4]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网