题目内容
(本小题满分12分)
已知f (x)=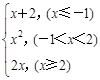 .
.
(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
(1)(-∞,+∞);(2) ;(3)见解析。
;(3)见解析。
解析试题分析:(1)注意分段函数定义域和值域的求法和要求,第一段值域为(-∞,1],第二段值域为(0,4),
第三段值域为[4,+∞),综上,函数的值域为(-∞,+∞). ……4分
(2)g (t)=3,即t+2=3,t≤-1,不存在;
x2=3,-1<x<2,解得:x= ,即t=
,即t= ;
;
2x=3,x≥2,x不存在.
综上,t的值为 . ……8分
. ……8分
(3)因为函数在[2,+∞)上的解析式为f (x)=2x,任取x1,x2∈[2,+∞),且x1<x2,则
f (x1)-f (x2)=2x1-2x2=2(x1-x2)<0,所以函数在[2,+∞)上单调递增. ……12分
考点:本题考查分段函数、利用定义证明函数的单调性。
点评:分段函数的值域是各段表达式的y值的并集。

练习册系列答案
相关题目
 是定义在
是定义在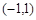 上的奇函数,当
上的奇函数,当 时
时 且
且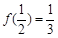 。
。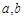 的值;
的值;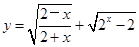 的定义域为
的定义域为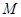 ,
,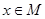 时,求函数
时,求函数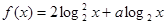 的最大值。
的最大值。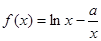 。
。 的单调区间;
的单调区间;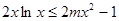 在
在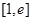 恒成立,求
恒成立,求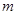 的取值范围。
的取值范围。 。
。 的定义域;
的定义域;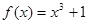 为R上的单调递增函数
为R上的单调递增函数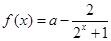 (其中常数
(其中常数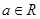 )
) 的单调性,并加以证明;
的单调性,并加以证明; 的值。
的值。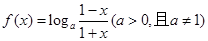
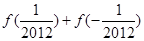 的值;
的值;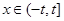 (其中
(其中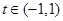 ,且
,且 为常数)时,
为常数)时,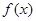 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如 时,求满足不等式
时,求满足不等式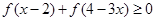 的
的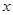 的范围.
的范围. 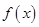 是定义在
是定义在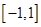 上的奇函数,且
上的奇函数,且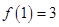 ,若
,若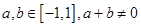 时,有
时,有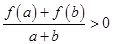 成立.
成立.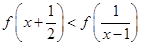 ;
;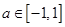 时,
时,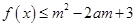 对所有的
对所有的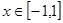 恒成立,求实数
恒成立,求实数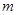 的取值范围.
的取值范围.