题目内容
10.设x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{x+y≥4}\\{2x-y≤1}\end{array}\right.$,则z=x-y的取值范围为(-∞,$-\frac{2}{3}$].分析 先根据不等式组画出该不等式组表示的平面区域,而由z=x-y得y=x-z,可将该式看成斜率为1,在y轴上的截距为-z的一族平行直线的方程,并且得到直线y=x-z的截距增大时,z减小,结合平面区域即可知道当直线y=x-z经过直线x+y=4和直线2x-y=1的交点时z取到最大值,并且可以无限变小,这样即可得出z的取值范围.
解答 解:原不等式所表示的平面区域如下图阴影部分所示: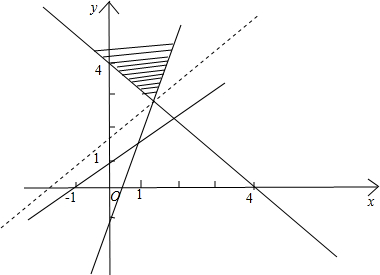
由z=x-y得,y=x-z,该方程便表示斜率为1,在y轴上截距为-z的一族平行直线;
∴截距最小z便最大;
由$\left\{\begin{array}{l}{x+y=4}\\{2x-y=1}\end{array}\right.$得阴影部分的下端点为($\frac{5}{3},\frac{7}{3}$);
∴直线y=x-z经过下端点时z取最大值-$\frac{2}{3}$;
此时随着虚线向上平移截距不断增大,而z不断减小;
∴z的取值范围为(-∞,-$\frac{2}{3}$].
故答案为:(-∞,-$\frac{2}{3}$].
点评 考查不等式组表示一个平面区域,并能够正确找出不等式组所表示的平面区域,以及数形结合解题的方法,掌握线性规划问题的解决方法与过程,直线在y轴上的截距的概念及求法,知道y=x-z表示一族平行直线.

练习册系列答案
相关题目
1.点A在点B的上方,从A看B的俯角为α,从B看A的仰角为β,则( )
| A. | α=β | B. | α+β=$\frac{π}{2}$ | C. | α+β=π | D. | α>β |
5.已知△ABC的顶点A的坐标为(3,-1),∠B,∠C的平分线所在的直线方程分别是x=0,y=2x,则BC边所在的直线方程为( )
| A. | x+7y+20=0 | B. | x-7y+20=0 | C. | 7x-y+20=0 | D. | 7x+y+20=0 |