题目内容
20.设函数f(x)的定义域为R+,对任意x,y∈R+,有f(x•y)=f(x)+f(y),已知f(2)=a,f(5)=b,求f(200)的值.分析 利用赋值法是常用的方法,f(200)=f(2)+f(100)=f(2)+f(2)+f(50)+3f(2)+f(25)=3f(2)+2f(5),问题得以解决.
解答 解:∵f(x•y)=f(x)+f(y),f(2)=a,f(5)=b,
∴f(200)=f(2)+f(100)=f(2)+f(2)+f(50)=3f(2)+f(25)=3f(2)+2f(5)=3a+2b.
点评 本题考查了抽象函数的求值问题,灵活赋值是关键,属于基础题.

练习册系列答案
相关题目
2.已知f(x+1)=x-1+ex+1,则函数f(x)在点(0,f(0))处的切线与坐标轴围成的三角形的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
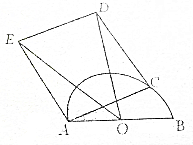 如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.
如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.