题目内容
11.在极坐标系中,已知射线C1:θ=$\frac{π}{6}$(ρ≥0),动圆C2:ρ2-2x0ρcosθ+x02-4=0(x0∈R).(1)求C1,C2的直角坐标方程;
(2)若射线C1与动圆C2相交于M与N两个不同点,求x0的取值范围.
分析 (1)利用tan θ=$\frac{y}{x}$,θ=$\frac{π}{6}$(ρ≥0),即可得出C1的直角坐标方程.利用$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}$,即可得出C2的直角坐标方程.
(2)联立$\left\{\begin{array}{l}{θ=\frac{π}{6},ρ≥0}\\{{ρ}^{2}-2{x}_{0}ρcosθ+{{x}_{0}}^{2}-4=0,{x}_{0}∈R}\end{array}\right.$,由于关于ρ的一元二次方程ρ2-$\sqrt{3}$x0ρ+x02-4=0(x0∈R)在[0,+∞)内有两个实根.可得$\left\{\begin{array}{l}{△=3{x}_{0}^{2}-4({x}_{0}^{2}-4)>0}\\{{ρ}_{1}+{ρ}_{2}=\sqrt{3}{x}_{0}>0}\\{{ρ}_{1}{ρ}_{2}≥0}\end{array}\right.$,解出即可得出.
解答 解:(1)∵tan θ=$\frac{y}{x}$,θ=$\frac{π}{6}$(ρ≥0),∴y=$\frac{\sqrt{3}}{3}$x(x≥0).
∴C1的直角坐标方程为y=$\frac{\sqrt{3}}{3}$x(x≥0).
∵$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}$,∴C2的直角坐标方程x2+y2-2x0x+x02-4=0.
(2)联立$\left\{\begin{array}{l}{θ=\frac{π}{6},ρ≥0}\\{{ρ}^{2}-2{x}_{0}ρcosθ+{{x}_{0}}^{2}-4=0,{x}_{0}∈R}\end{array}\right.$
关于ρ的一元二次方程ρ2-$\sqrt{3}$x0ρ+x02-4=0(x0∈R)在[0,+∞)内有两个实根.
即$\left\{\begin{array}{l}{△=3{x}_{0}^{2}-4({x}_{0}^{2}-4)>0}\\{{ρ}_{1}+{ρ}_{2}=\sqrt{3}{x}_{0}>0}\\{{ρ}_{1}{ρ}_{2}≥0}\end{array}\right.$,
得$\left\{\begin{array}{l}{-4<{x}_{0}<4}\\{{x}_{0}>2}\\{{x}_{0}≥2或{x}_{0}≤-2}\end{array}\right.$,
解得2≤x0<4.
点评 本题考查了极坐标化为直角坐标方程的方法、曲线的交点坐标、极坐标方程的应用、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案(i)存在直线m在点P(x0,y0)处与曲线C相切;
(ii)曲线C在点P附近位于直线m的两侧.则称点P为曲线C的“相似拐点”.
下列命题不正确的是( )
| A. | 点P(0,0)为曲线C:y=x3的“相似拐点” | |
| B. | 点P(0,0)为曲线C:y=sinx的“相似拐点” | |
| C. | 点P(0,0)为曲线C:y=tanx的“相似拐点” | |
| D. | 点P(1,0)为曲线C:y=lnx的“相似拐点” |
| A. | 奇函数,且在(0,1)上是增函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 偶函数,且在(0,1)上是减函数 |
| A. | b>c>a | B. | a>c>b | C. | b>a>c | D. | a>b>c |

| A. | [0,π] | B. | [$\frac{π}{2}$,$\frac{3π}{2}$] | C. | [0,$\frac{3π}{2}$] | D. | [$\frac{π}{2}$,2π] |
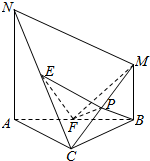 已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.
已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.