题目内容
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.
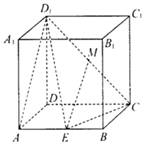
(1)当E点是AB中点时,求证:直线ME‖平面ADD1 A1;
(2)若二面角AD1EC的余弦值为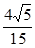 .求线段AE的长.
.求线段AE的长.
【答案】
(1)证明:见解析;(2)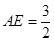 .
.
【解析】
试题分析:(1)证明:取 的中点N,连结MN、AN、
的中点N,连结MN、AN、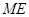 ,由三角形中位线定理得到
,由三角形中位线定理得到
MN∥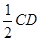 ,AE∥
,AE∥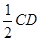 ,所以四边形MNAE为平行四边形,可知 ME∥AN,即得证.
,所以四边形MNAE为平行四边形,可知 ME∥AN,即得证.
(2)利用空间向量.
设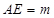 ,建立空间直角坐标系,将问题转化成计算平面的“法向量”夹角的余弦,建立
,建立空间直角坐标系,将问题转化成计算平面的“法向量”夹角的余弦,建立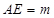 的方程.
的方程.
试题解析:((1)证明:取 的中点N,连结MN、AN、
的中点N,连结MN、AN、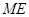 ,
1分
,
1分
MN∥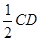 ,AE∥
,AE∥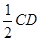 ,
3分
,
3分
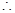 四边形MNAE为平行四边形,可知 ME∥AN
4分
四边形MNAE为平行四边形,可知 ME∥AN
4分


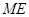 ∥平面
∥平面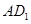 .
6分
.
6分
(2)设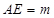 ,如图建立空间直角坐标系 7分
,如图建立空间直角坐标系 7分

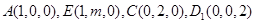 ,
,
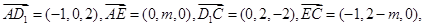 平面
平面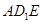 的法向量为
的法向量为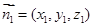 ,由
,由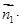
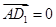 及
及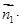
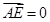 得
得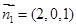 9分
9分
平面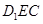 的法向量为
的法向量为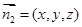 ,由
,由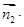
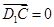 及
及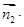
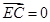 得
得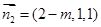 11分
11分
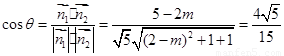 ,即
,即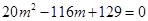 ,解得
,解得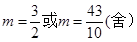
所以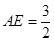 12分
12分
考点:直线与平面平行的判定,二面角,距离的计算,空间向量的应用.

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.