题目内容
函数 的定义域为A,若
的定义域为A,若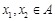 且
且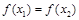 时总有
时总有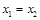 ,则称
,则称  为单函数.例如,函数
为单函数.例如,函数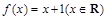 是单函数.下列命题:
是单函数.下列命题:
①函数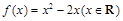 是单函数;②函数
是单函数;②函数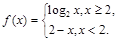 是单函数;
是单函数;
③若 为单函数,
为单函数,  且
且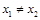 ,则
,则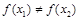 ;
;
④若函数 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
③
解析试题分析:解:命题①中,因为 ,所以
,所以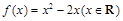 不是单函数, 命题①为假命题;
不是单函数, 命题①为假命题;
命题②中,因为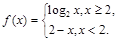 所以,
所以, ,所以
,所以 不是单函数, 命题②为假命题;
不是单函数, 命题②为假命题;
因为“若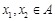 且
且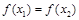 时总有
时总有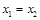 ”与命题“
”与命题“ 且
且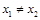 ,则
,则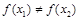 ;”互为逆不命题,故③为真命题;
;”互为逆不命题,故③为真命题;
由命题①②中的两个函数作为实例,说明若函数 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则 不一定是单函数.所以④是假命题.
不一定是单函数.所以④是假命题.
考点:1、新定义;2、函数的单调性;3、分段函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
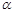 表示平面,m是
表示平面,m是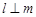 ”是“
”是“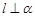 ”成立的 条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个)
”成立的 条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个)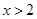 ”是“
”是“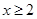 ”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)
”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)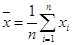 ,
,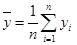 ,则回归直线y=bx+a必过点(
,则回归直线y=bx+a必过点( ,
, 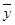 ).
).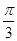 个单位,得到函数y=sin
个单位,得到函数y=sin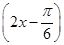 的图象;
的图象;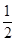 >0.则命题“p∧(
>0.则命题“p∧(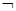 q)”是假命题;
q)”是假命题;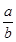 =-3;
=-3;