题目内容
已知⊙O:x2+y2=25与⊙O1:x2+y2-6
x+6
y+11=0关于直线l对称,则直线l被⊙O截得的线段长为( )
| 2 |
| 2 |
分析:先确定直线l方程,再计算O到直线的距离,即可求得直线l被⊙O截得的线段长.
解答:解:⊙O:x2+y2=25的圆心坐标为(0,0),半径为5;⊙O1:x2+y2-6
x+6
y+11=0的圆心坐标为(3
,-3
)
∴OO1的垂直平分线方程为:x-y-3
=0
∵⊙O:x2+y2=25与⊙O1:x2+y2-6
x+6
y+11=0关于直线l对称,
∴直线l方程为:x-y-3
=0
∴O到直线的距离为
=3
∴直线l被⊙O截得的线段长为2
=8
故选D.
| 2 |
| 2 |
| 2 |
| 2 |
∴OO1的垂直平分线方程为:x-y-3
| 2 |
∵⊙O:x2+y2=25与⊙O1:x2+y2-6
| 2 |
| 2 |
∴直线l方程为:x-y-3
| 2 |
∴O到直线的距离为
|-3
| ||
|
∴直线l被⊙O截得的线段长为2
| 52-32 |
故选D.
点评:本题考查圆与圆,直线与圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
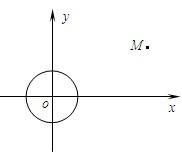 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2). 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.