题目内容
 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)已知⊙O:x2+y2=r2(r>0)的切线l总与曲线C有两个交点M、N,并且其中一条切线满足∠MON>90°,求证:对于任意一条切线l总有∠MON>90°.
分析:( I)由题意,|QA|+|QB|=|QP|+|QB|=6,所以Q点轨迹是以A、B为焦点的椭圆,故可求曲线C的轨迹方程;
( II)先考虑切线的斜率存在的情形.设切线l:y=kx+m,利用l与⊙O相切,建立方程,再由
,消去y,借助于韦达定理,证明
•
=
<0即可,再考虑两种特殊情况:(1)当满足∠MON>90°的那条切线斜率不存在时,切线方程为x=±r,(2)当满足∠MON>90°的那条切线斜率存在时,故结论可证.
( II)先考虑切线的斜率存在的情形.设切线l:y=kx+m,利用l与⊙O相切,建立方程,再由
|
| OM |
| ON |
| 14m2-45(1+k2) |
| 5+9k2 |
解答:( I)解:由题意,|QA|+|QB|=|QP|+|QB|=6,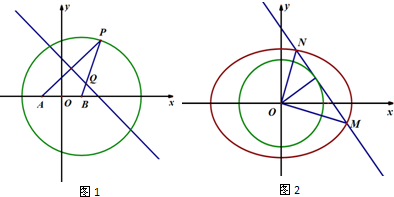
∴Q点轨迹是以A、B为焦点的椭圆,且a=3,c=2,
∴曲线C的轨迹方程是
+
=1.(5分)
( II)证明:先考虑切线的斜率存在的情形.设切线l:y=kx+m,则
由l与⊙O相切得
=r即m2=r2(1+k2)①(7分)
由
,消去y得,(5+9k2)x2+18kmx+9(m2-5)=0,
设M(x1,y1),N(x2,y2),则由韦达定理得x1+x2=-
,x1x2=
(9分)
•
=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2
=
-
+m2=
②(10分)
由于其中一条切线满足∠MON>90°,对此
•
=
<0
结合①式m2=r2(1+k2)可得r2>
(12分)
于是,对于任意一条切线l,总有m2>
(1+k2),进而
•
=
<0
故总有∠MON>90°.(14分)
最后考虑两种特殊情况:
(1)当满足∠MON>90°的那条切线斜率不存在时,切线方程为x=±r.代入椭圆方程可得交点的纵坐标y=±
,
因∠MON>90°,故r<
,得到r2>
,同上可得:任意一条切线l均满足∠MON>90°;
(2)当满足∠MON>90°的那条切线斜率存在时,r2>
,r<
,对于斜率不存在的切线x=±r也有∠MON>90°.
综上所述,命题成立.(15分)

∴Q点轨迹是以A、B为焦点的椭圆,且a=3,c=2,
∴曲线C的轨迹方程是
| x2 |
| 9 |
| y2 |
| 5 |
( II)证明:先考虑切线的斜率存在的情形.设切线l:y=kx+m,则
由l与⊙O相切得
| |m| | ||
|
由
|
设M(x1,y1),N(x2,y2),则由韦达定理得x1+x2=-
| 18km |
| 5+9k2 |
| 9(m2-5) |
| 5+9k2 |
| OM |
| ON |
=
| 9(1+k2)(m2-5) |
| 5+9k2 |
| 18k2m2 |
| 5+9k2 |
| 14m2-45(1+k2) |
| 5+9k2 |
由于其中一条切线满足∠MON>90°,对此
| OM |
| ON |
| 14m2-45(1+k2) |
| 5+9k2 |
结合①式m2=r2(1+k2)可得r2>
| 45 |
| 14 |
于是,对于任意一条切线l,总有m2>
| 45 |
| 14 |
| OM |
| ON |
| 14m2-45(1+k2) |
| 5+9k2 |
故总有∠MON>90°.(14分)
最后考虑两种特殊情况:
(1)当满足∠MON>90°的那条切线斜率不存在时,切线方程为x=±r.代入椭圆方程可得交点的纵坐标y=±
5-
|
因∠MON>90°,故r<
5-
|
| 45 |
| 14 |
(2)当满足∠MON>90°的那条切线斜率存在时,r2>
| 45 |
| 14 |
5-
|
综上所述,命题成立.(15分)
点评:本题考查曲线轨迹的求解,考查椭圆的标准方程,考查直线与圆、椭圆的位置关系,考查学生分析解决问题的能力,需要一定的基本功.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
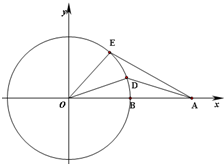 如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π
如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
 ,求四边形ODAE的面积;
,求四边形ODAE的面积;