题目内容

（2012•黄州区模拟）已知⊙O：x2+y2=4及点A（1，3），BC为⊙O的任意一条直径，则
AB
•
AC
=（　　）
分析：由题意可得|OB|=|OC|=2，|AO|=
10
． 设∠AOB=θ，则∠AOC=π-θ．再根据
AB
•
AC
=（
AO
+
OB
）•（
AO
+
OC
），利用两个向量的数量积的定义求得结果．
解答：解：由题意可得|OB|=|OC|=2，|AO|=
10
． 设∠AOB=θ，则∠AOC=π-θ．
∴
AB
•
AC
=（
AO
+
OB
）•（
AO
+
OC
）=
AO
2+
AO
•
OB
+
AO
•
OC
+
OB
•
OC

=10+
10
×2cosθ+
10
×2cos（π-θ）+2×2cosπ=6，
故选A．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，属于中档题．
练习册系列答案
相关题目
（2012•黄州区模拟）已知向量
m
=（cos
x
2
，-1），
n
=（
3
sin
x
2
，cos2
x
2
），设函数f（x）=
m
•
n
+1．
（1）若x∈[0，
π
2
]，f（x）=
11
10
，求cosx的值；
（2）在△ABC中，角A，B，C的对边分别是a，b，c，且满足2bcosA≤2c-
3
a，求f（x）的取值范围．
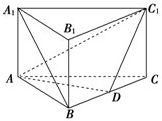（2012•黄州区模拟）如图，在直三棱柱ABC-A1B1C1中，AB=BC=2AA1，∠ABC=90°，D是BC的中点．
（Ⅰ）求证：A1B∥平面ADC1；
（Ⅱ）求二面角C1-AD-C的余弦值；
（Ⅲ）试问线段A1B1上是否存在点E，使AE与DC1成60°角？若存在，确定E点位置，若不存在，说明理由．
（2012•黄州区模拟）已知某几何体的三视图如图，则该几何体的表面积为
3+
2
+
3
3+
2
+
3
．
（2012•黄州区模拟）已知函数f（x）=
|log
x
4
-1|-2，|x|≤1
1
1+x
1
3
，|x|＞1
，则f（f（27））=（　　）
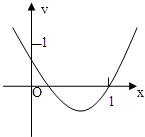（2012•黄州区模拟）如图是二次函数f（x）=x2-bx+a的部分图象，则函数g（x）=2lnx+f（x）在点（b，g（b））处切线的斜率的最小值是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网