题目内容
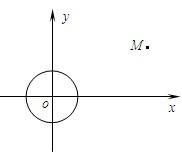 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2).(Ⅰ)过点M向⊙O引切线l,求直线l的方程;
(Ⅱ)求以点M为圆心,且被直线y=2x-1截得的弦长为4的⊙M的方程;
(Ⅲ)设P为(Ⅱ)中⊙M上任一点,过点P向⊙O引切线,切点为Q.试探究:平面内是否存在一定点R,使得
| PQ | PR |
分析:(Ⅰ)找出圆的圆心坐标和半径,设切线方程的斜率为k,由M的坐标和k写出切线l的方程,然后利用点到直线的距离公式表示出圆心到直线l的距离d让d等于半径r得到关于k的方程,求出方程的解即可得到k的值,写出直线l的方程即可;
(Ⅱ)根据点到直线的距离公式求出M到已知直线的距离d,然后利用勾股定理即可求出圆M的半径,根据圆心和半径写出圆的标准方程即可;
(Ⅲ)假设存在这样的R点,设出R的坐标,并设出P的坐标,根据圆的切线垂直于过切点的半径得到三角形OPQ为直角三角形,根据勾股定理表示出PQ的长,然后利用两点间的距离公式表示出PR的长,设PQ与PR之比等于λ,把PQ和PR的式子代入后两边平方化简得到一个关系式记作(*),又因为P在⊙M上,所以把P的坐标当然到⊙M的方程中,化简后代入到(*)中,根据多项式对应项的系数相等即可求出R的坐标和λ的值.
(Ⅱ)根据点到直线的距离公式求出M到已知直线的距离d,然后利用勾股定理即可求出圆M的半径,根据圆心和半径写出圆的标准方程即可;
(Ⅲ)假设存在这样的R点,设出R的坐标,并设出P的坐标,根据圆的切线垂直于过切点的半径得到三角形OPQ为直角三角形,根据勾股定理表示出PQ的长,然后利用两点间的距离公式表示出PR的长,设PQ与PR之比等于λ,把PQ和PR的式子代入后两边平方化简得到一个关系式记作(*),又因为P在⊙M上,所以把P的坐标当然到⊙M的方程中,化简后代入到(*)中,根据多项式对应项的系数相等即可求出R的坐标和λ的值.
解答:解:(Ⅰ)由⊙O:x2+y2=1得到圆心O(0,0)半径r=1,
设切线l方程为y-2=k(x-4),
易得
=1,解得k=
,
∴切线l方程为y-2=
(x-4);
(Ⅱ)圆心M到直线y=2x-1的距离d=
=
,
设圆的半径为r,则r2=22+(
)2=9,
∴⊙M的方程为(x-4)2+(y-2)2=9;
(Ⅲ)假设存在这样的点R(a,b),点P的坐标为(x,y),相应的定值为λ,
根据题意可得PQ=
,
∴
=λ,
即x2+y2-1=λ2(x2+y2-2ax-2by+a2+b2)(*),
又点P在圆上∴(x-4)2+(y-2)2=9,
即x2+y2=8x+4y-11,代入(*)式得:
8x+4y-12=λ2[(8-2a)x+(4-2b)y+(a2+b2-11)],
若系数对应相等,则等式恒成立,∴
,
解得a=2,b=1,λ=
或a=
,b=
,λ=
,
∴可以找到这样的定点R,使得
为定值.
如点R的坐标为(2,1)时,比值为
;点R的坐标为(
,
)时,比值为
.
设切线l方程为y-2=k(x-4),
易得
| |4k-2| | ||
|
8±
| ||
| 15 |
∴切线l方程为y-2=
8±
| ||
| 15 |
(Ⅱ)圆心M到直线y=2x-1的距离d=
| |5| | ||
|
| 5 |
设圆的半径为r,则r2=22+(
| 5 |
∴⊙M的方程为(x-4)2+(y-2)2=9;
(Ⅲ)假设存在这样的点R(a,b),点P的坐标为(x,y),相应的定值为λ,
根据题意可得PQ=
| x2+y2-1 |
∴
| ||
|
即x2+y2-1=λ2(x2+y2-2ax-2by+a2+b2)(*),
又点P在圆上∴(x-4)2+(y-2)2=9,
即x2+y2=8x+4y-11,代入(*)式得:
8x+4y-12=λ2[(8-2a)x+(4-2b)y+(a2+b2-11)],
若系数对应相等,则等式恒成立,∴
|
解得a=2,b=1,λ=
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
| ||
| 3 |
∴可以找到这样的定点R,使得
| PQ |
| PR |
如点R的坐标为(2,1)时,比值为
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
| ||
| 3 |
点评:此题考查学生掌握直线与圆的位置关系,灵活运用两点间的距离公式及点到直线的距离公式化简求值,会根据圆心坐标和圆的半径写出圆的标准方程,是一道综合题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.