题目内容
(本题满分16分)
在区间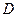 上,如果函数
上,如果函数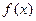 为增函数,而函数
为增函数,而函数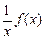 为减函数,则称函数
为减函数,则称函数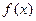 为“弱增”函数.已知函数
为“弱增”函数.已知函数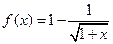
(1)判断函数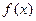 在区间
在区间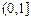 上是否为“弱增”函数
上是否为“弱增”函数
(2)设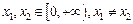 ,证明
,证明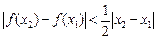
(3)当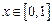 时,不等式
时,不等式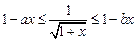 恒成立,求实数
恒成立,求实数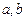 的取值范围
的取值范围
在区间
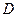 上,如果函数
上,如果函数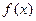 为增函数,而函数
为增函数,而函数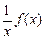 为减函数,则称函数
为减函数,则称函数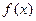 为“弱增”函数.已知函数
为“弱增”函数.已知函数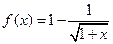
(1)判断函数
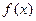 在区间
在区间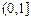 上是否为“弱增”函数
上是否为“弱增”函数(2)设
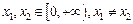 ,证明
,证明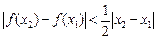
(3)当
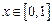 时,不等式
时,不等式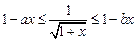 恒成立,求实数
恒成立,求实数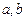 的取值范围
的取值范围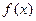 在区间
在区间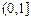 为“弱增”函数
为“弱增”函数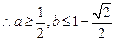
(1)显然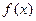 在区间
在区间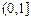 为增函数,……..1分
为增函数,……..1分
 ,……..4分
,……..4分
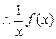 为减函数.
为减函数.
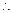
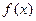 在区间
在区间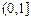 为“弱增”函数. ……………………..5分
为“弱增”函数. ……………………..5分
(2)
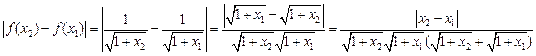
……..8分
 ,
,
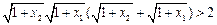 ,.……..9分
,.……..9分
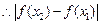
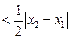 . .……..10分
. .……..10分
(3)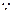 当
当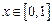 时,不等式
时,不等式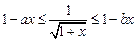 恒成立.
恒成立.
当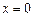 时,不等式显然成立. ……..12分
时,不等式显然成立. ……..12分
当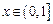 时.等价于:
时.等价于: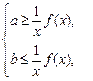 ……..14分
……..14分
由(1)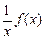 为减函数,
为减函数, 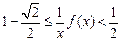 ,
,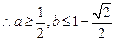 .……..16分
.……..16分
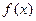 在区间
在区间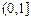 为增函数,……..1分
为增函数,……..1分 ,……..4分
,……..4分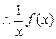 为减函数.
为减函数.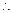
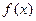 在区间
在区间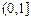 为“弱增”函数. ……………………..5分
为“弱增”函数. ……………………..5分(2)
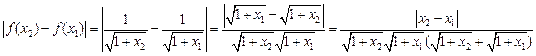
……..8分
 ,
,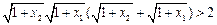 ,.……..9分
,.……..9分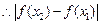
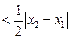 . .……..10分
. .……..10分(3)
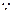 当
当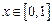 时,不等式
时,不等式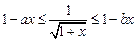 恒成立.
恒成立.当
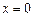 时,不等式显然成立. ……..12分
时,不等式显然成立. ……..12分当
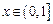 时.等价于:
时.等价于: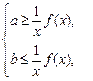 ……..14分
……..14分由(1)
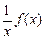 为减函数,
为减函数, 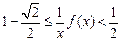 ,
,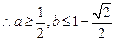 .……..16分
.……..16分
练习册系列答案
相关题目
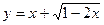 的值域是
的值域是 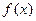 在区间
在区间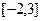 是增函数,则
是增函数,则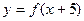 的递增区间是
的递增区间是 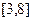
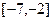
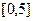
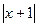 ,在(-1,0)上有f(x)>0,那么 ( )
,在(-1,0)上有f(x)>0,那么 ( )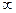 ,0)上是增函数
,0)上是增函数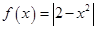 ,若0<a<b,且f(a)=f(b),则ab的取值范围是 ( )
,若0<a<b,且f(a)=f(b),则ab的取值范围是 ( )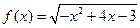 的单调递减区间是
的单调递减区间是 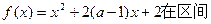 (—∞,4]是减函数,则实数
(—∞,4]是减函数,则实数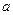 的取值范围是( )
的取值范围是( )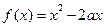 定义在区间
定义在区间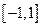 上,则
上,则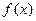 是单调函数的充要条件是
是单调函数的充要条件是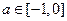
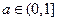
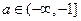
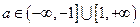
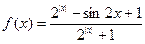 在[-a,a](a>0)上的最大值为m,最小值为n,则m+n= 。
在[-a,a](a>0)上的最大值为m,最小值为n,则m+n= 。