题目内容
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这5 个球投放在这5个盒内,要求每个盒内投放一个球,并且恰有两个球的编号与盒子的编号相同,则这样的投放方法的总数为( )
| A.20 | B.30 | C.60 | D.120 |
A
解析试题分析:本题是一个排列、组合及简单计数问题,只有两个小球的编号与盒子号一致,则首先从5个号码中,选出两个号码,有 =10种结果,其余的三个盒子与小球的编号不同,则第一个球有两种选择,另外两个球的位置确定,共有2种结果,相乘得到结果.解:由题意知本题是一个排列、组合及简单计数问题,有且只有两个小球的编号与盒子号一致,则首先从5个号码中,选出两个号码,有
=10种结果,其余的三个盒子与小球的编号不同,则第一个球有两种选择,另外两个球的位置确定,共有2种结果,相乘得到结果.解:由题意知本题是一个排列、组合及简单计数问题,有且只有两个小球的编号与盒子号一致,则首先从5个号码中,选出两个号码,有 =10种结果,其余的三个小球与盒子的编号不同,则第一个小球有两种选择,另外两个小球的位置确定,编号不同的放法共有2种结果,根据分步计数原理得到共有10×2=20种结果,故答案为A
=10种结果,其余的三个小球与盒子的编号不同,则第一个小球有两种选择,另外两个小球的位置确定,编号不同的放法共有2种结果,根据分步计数原理得到共有10×2=20种结果,故答案为A
考点:排列组合及简单计数问题
点评:本题考查排列组合及简单计数问题,这是一个典型的排列组合问题,本题解题的关键是当两个相同的号码确定以后,其余的三个号码不同的排法共有2种结果,这里容易出错,本题是一个中档题目

练习册系列答案
相关题目
现需编制一个八位的序号,规定如下:序号由4个数字和2个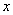 、1个
、1个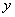 、1个
、1个 组成;2个
组成;2个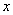 不能连续出现,且
不能连续出现,且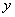 在
在 的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )
| A.12600 | B.6300 | C.5040 | D.2520 |
将4本不同的书全发给3名同学,则每名同学至少有一本书的概率为( )
A. | B.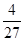 | C. | D. |
 展开式中x的系数为 ( )
展开式中x的系数为 ( )
| A.-150 | B.150 | C.300 | D.-300 |
设 ,那么
,那么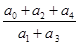 的值为( )
的值为( )
A.- | B.- | C.- | D.—1 |
由数字1,2,3,4,5组成没有重复数字的五位数,其中偶数共有 ( )
| A.60个 | B.48个 | C.36个 | D.24个 |
用数字1,2,3,4组成数字可以重复的四位数,其中有且只有一个数字出现两次的四位数的个数为
| A.144 | B.120 | C.108 | D.72 |
 的展开式中,只有第5项的二项式系数最大,则展开式中的第6项是 ()
的展开式中,只有第5项的二项式系数最大,则展开式中的第6项是 ()