题目内容
在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽出3件,至少有1件次品的抽法不正确的结果是( )
A. | B.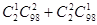 | C. | D. |
A
解析试题分析:解法一:根据题意,“至少有1件次品”可分为“有1件次品”与“有2件次品”两种情况,由组合数公式分别求得两种情况下的抽法数,进而相加可得答案.,解法二:“至少有1件次品”的对立事件是“三件都是合格品”,用事件总数减去“三件都是合格品”的种数.解:解法一:根据题意,“至少有1件次品”可分为“有1件次品”与“有2件次品”两种情况,,“有1件次品”的抽取方法有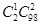 种,,“有2件次品”的抽取方法有
种,,“有2件次品”的抽取方法有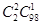 种,,则共有
种,,则共有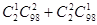 种不同的抽取方法,,解法二,“至少有1件次品”的对立事件是“三件都是合格品”,“三件都是合格品”的抽取方法有C983种,,∴抽出的3件中至少有1件是次品的抽法有
种不同的抽取方法,,解法二,“至少有1件次品”的对立事件是“三件都是合格品”,“三件都是合格品”的抽取方法有C983种,,∴抽出的3件中至少有1件是次品的抽法有 种,故选A
种,故选A
考点:组合数公式
点评:本题考查组合数公式的运用,解题时要注意“至少”“至多”“最少”“最少”等情况的分类讨论.

练习册系列答案
相关题目
若多项式 ,则
,则 ( )
( )
| A.1 | B.60 | C. | D. |
某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原节目单中,那么不同插法的种数为( )
| A.42 | B.30 | C.20 | D.12 |
甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有( )
| A.30种 | B.24种 | C.12种 | D.6种 |
 的展开式中,常数项等于( )
的展开式中,常数项等于( )
| A.15 | B.10 | C. | D.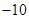 |
某班级有一个7人小组,现任选其中3人相互调整座位,其余4人座位不变,则不同的调整方案的种数有( )
| A.35 | B.70 | C.210 | D.105 |
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这5 个球投放在这5个盒内,要求每个盒内投放一个球,并且恰有两个球的编号与盒子的编号相同,则这样的投放方法的总数为( )
| A.20 | B.30 | C.60 | D.120 |
 的展开式中各项系数之和为64,则展开式的常数项为( )
的展开式中各项系数之和为64,则展开式的常数项为( )
| A.-540 | B.-162 | C.162 | D.540 |
在 的展开式中,
的展开式中, 的系数为( )
的系数为( )
A. | B. | C. | D. |