题目内容
（2008•和平区三模）已知函数f(x)=(
)x-log2x，若实数x0是方程f（x）=0的解，且0＜x1＜x0，则f（x1）的值（ ）
| 1 |
| 3 |
分析：方法1：由f（x）=0，得(
)x=log?2x，分别作出函数y=(
)x，y=log?2x的图象，利用图象确定f（x1）的值的情况．
方法2：（函数单调性法）判断出函数的单调性，由单调性即可判断出值的符号
| 1 |
| 3 |
| 1 |
| 3 |
方法2：（函数单调性法）判断出函数的单调性，由单调性即可判断出值的符号
解答：解：：方法1（函数图象法）
由f（x）=0，得(
)x=log?2x，分别作出函数y=(
)x，y=log?2x的图象，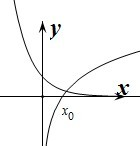
由图象可知，当0＜x1＜x0时，(
)x1＞log?2x1，所以f(x1)=(
)x1-log?2x1＞0．
故选C．
方法2：（函数单调性法）
因为函数y=(
)x是单调减函数，y=log?2x 在（0，+∞）上是增函数，所以根据函数单调性的性质可知，
数f(x)=(
)x-log2x，在（0，+∞）上是减函数．
因为0＜x1＜x0，所以f（x1）＞f（x0）=0，
故选C．
由f（x）=0，得(
| 1 |
| 3 |
| 1 |
| 3 |
由图象可知，当0＜x1＜x0时，(
| 1 |
| 3 |
| 1 |
| 3 |
故选C．
方法2：（函数单调性法）
因为函数y=(
| 1 |
| 3 |
数f(x)=(
| 1 |
| 3 |
因为0＜x1＜x0，所以f（x1）＞f（x0）=0，
故选C．
点评：本题主要考查函数值符合的判断，利用根的存在性定理，结合数形结合的思想求解是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
（2008•和平区三模）如图，在△ABC中，∠ABC=∠ACB=30°，AB，AC边上的高分别为CD，BE，则以B，C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为